| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 스토어드 프로시저
- 그래프
- Stored Procedure
- binary search
- Two Points
- 이진탐색
- Dijkstra
- DP
- Hash
- MYSQL
- String
- Brute Force
- 다익스트라
- two pointer
- union find
- Trie
- SQL
- Today
- Total
목록통계학/확률론 (3)
codingfarm
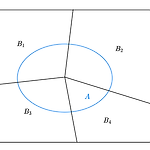 전체 확률 법칙(Law of total probability)
전체 확률 법칙(Law of total probability)
표본공간 $S$를 $n$개로 분할하여 사상 $\{B_1,B_2,\cdots,B_n\}$를 얻는다. $P(B \neq 0),\;\;\;i=1,2,\cdots,n$ 일때 $S$의 임의의 사건 $A$에 대해 $$P(A)=\sum_{i=1}^{n}P(B_i \cap A)=\sum_{i=1}^{n}P(B_i)P(A|B_i)$$ 표본 공간 $S$가 아래와 같이 주어진다. 표본공간 $S$가 $n$개의 사상 $\{B_1, B_2, B_3, B_4\}$로 분할되어 있다. 그리고 사상 $A$가 표본공간 $S$의 임의의 사상이다. 그림에서 보다시피 $A=(B_1 \cap A)\cup (B_2 \cap A)\cup (B_3 \cap A)\cup (B_4 \cap A)$ 사건 $A$의 확률을 교집합의 합집합으로 나타낼 수 있다..
$P(B)>0$ 일때 사상 $B$가 발생했다는 조건하에 사상 $A$가 일어날 확률을 조건부확률(Conditional probability)라 한다. $$P(A|B)=\dfrac{P(A \cap B)}{P(B)}$$ 두개의 사상 $A$와 $B$가 모두 일어날 확률 $P(A \cap B)$는 곱의 법칙(Multiplication rule)에 의해 아래와 같이 정의된다. $P(A) > 0$ 일때 $P(A \cap B) =P(A)P(B|A)$ $P(B) > 0$ 일때 $P(A \cap B)=P(B)P(A|B)$ 한 사상의 발생여부가 다른 사상의 발생에 영햐을 주지 않는 경우를 독립사상(independent event)라 한다. 사상 $A$와 $B$가 독립이면 $P(B|A)=P(B)$ $P(A|B)=P(A)$ 이..
 베이즈 정리(Bayes' theorem)
베이즈 정리(Bayes' theorem)
$n$개의 사상 $\{B_1,B_2,\cdots,B_n \}$이 표본공간 $S$의 분할이다. 사상 $A$가 표본공간 $S$의 임의의 사건이라면 $$P(B_i|A)=\dfrac{P(B_i)P(A|B_i)}{\sum_{i=1}^{n}P(B_i)P(A|B_i)}$$ 사상 $B_1,B_2,\cdots,B_n$이 표본공간 $S$의 분할(Partition)이라하자. 즉, $S=B_1 \cup B_2 \cup \cdots\cup B_n$ 그리고 $B_i \cap B_j \neq \varnothing,\;\;\; i \neq j$ 이때 $B_1, B_2, \cdots, B_m$은 상호 배반(matually exclusively)이며 포괄적(exhaustive)이다. 그러므로 $B_i \cap B_j = \varnoth..
