| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Brute Force
- 스토어드 프로시저
- Trie
- union find
- 이진탐색
- SQL
- 그래프
- Hash
- DP
- MYSQL
- two pointer
- Dijkstra
- Stored Procedure
- binary search
- String
- 다익스트라
- Two Points
- Today
- Total
목록통계학/수리통계학 (15)
codingfarm
 4.3 조건부 분포(Conditional Distribution)
4.3 조건부 분포(Conditional Distribution)
X와 Y가 공간 S에서 jointpmff(x,y)를 가진다. marginal pmf는 공간 SX와 SY에서 각각 fX(x),fY(y)이다. 사건(event)A={X=x},B={Y=y},(x,y)∈S일때 A∩B={X=x,Y=y} 이다. 왜냐하면 P(A∩B)=P(X=x,Y=y)=f(x,y) 그리고 P(B)=P(Y=y)=fY(y)>0(sinceY∈SY) 일 경우 사건 B가 주어질때 사건 A의 조건부확률(Conditional Probability)는 P(A|B)=P(A∩B)P(B)=f(x,y)fY(y)..
 피어슨 상관 계수(Pearson Correlation Coefficient)
피어슨 상관 계수(Pearson Correlation Coefficient)
∙ (피어슨)상관 계수는 두 변수가 서로 (선형)상관관계를 가지는지 확인하는 척도이다. ∙ 1이나 -1에 가까우면 상관관계가 있다 보고 0이면 없다고 본다. ∙ [−1,1]을 벗어나지 않는다. 다음과 같이 정의된 ρ=ρ(X,Y) 를 피어스 상관계수(pearson correlation coefficient)라고 한다. ρ=Cov(X,Y)σXσY=σXYσXσY,−1≤ρ≤1 Cov(X,Y)를 X와 Y의 공분산(covariance)라 한다. $Cov(X,Y) = E[(X-\mu_X)(..
 이산형 이변량 분포(Bivariate Distribution of The Discrete Type)
이산형 이변량 분포(Bivariate Distribution of The Discrete Type)
이산형 이변량 분포(Bivariate Distribution of The Discrete Type) ∙ 두개 이상의 확률변수에 대한 분포에 대해 다뤄본다 ex) 대학 입시에서 내신성적 X와 수능성적 Y의 관계 → 대학교성적 Z의 예측 가능 여부 확인 초등학생의 키(X), 몸무게(Y), 발사이즈(Z)간의 관계 → 성인이 됐을때의 키 W 예측 가능한가? X,Y를 이산형 확률 공간에서 정의된 두개의 확률 변수라 하고 X와 Y에 대응하는 2차원 공간을 S라 하자. X=x, Y=y인 확률을 f(x,y)=P(X=x,Y=y) 라 하면, f(x,y)는 X와 Y의 결합확률질량함수(joint probability..
 정규 분포(Normal Distribution)
정규 분포(Normal Distribution)
정규분포 규모가 큰 모집단을 관측할 때 많은 변수들이 종모양의 상대분포를 가질경우, 이런 변수들을 근사하는데 유용한 확률분포이다. 확률 변수 X라 정규분포를 따를경우 X의 pdf는 아래와 같다. $$f(x) = \dfrac{1}{\sigma \sqrt{2\pi}} \exp{\left[ - \dfrac{(x - \mu)^2}{2 \sigma ^2} \right]},~~~~~~-\infty
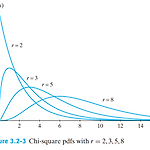 연속형 확률분포 - 카이제곱분포(chi-square distribution)
연속형 확률분포 - 카이제곱분포(chi-square distribution)
카이제곱 분포는 감마분포에서 θ=2,α=r2(rispositiveinteger)을 가지는 특수한 분포를 가리킨다. 확률변수 X의 pdf는 f(x)=1Γ(r/2)2r/2x(r/2)−1e−x/2,0<x<∞ X는 자유도(degree of freedom) r의 카이제곱분포를 따른다 하고 χ2(r)이라 표기한다. 평균과 분산 μ=r,σ2=αθ2=2r 자유도 r과 x값에 대한 카이제곱 cdf $$F(x)= \int_{0}^{x} \frac{1}{\Gamma(r/2)2^{r/2}}w^..
 연속형 확률분포 - 감마분포(The Gamma Distributions)
연속형 확률분포 - 감마분포(The Gamma Distributions)
∙ 평균 λ를 갖는 (근사)포아송과정에서 첫발생이 일어날때까지의 시간/간격은 지수분포를 가진다. ∙ α개의 발생이 일어날때까지 시간/공간을 w라 할때 확률변수 w는 감마분포를 따른다. 감마분포의 pdf, cdf, 특성값 f(w)=λ(λw)α−1(α−1)!e−λw F(w)=1−α−1∑k=0(λw)ke−λwk! 시간을 x로 치환하고 감마함수로 표현하면 $$f(x)=\dfrac{1}{\Gamma(\alpha) \theta^\alpha}x^{\alpha-1}e^{-x/\..
 연속형 확률분포 - 지수분포(The Exponential Distributions)
연속형 확률분포 - 지수분포(The Exponential Distributions)
지수 분포(Exponential Distributions) 이산형 확률변수의 포아송분포와 관련된 연속형 분포에 대해 알아보겠다. 주어진 구간에서 발생건수는 포아송분포를 갖는 이산형 확률변수이다. 여기서 연속되는 발생 사이의 대기시간은 연속형의 확률변수이다. 확률변수 X가 지수분포(exponential distribution)을 가질경우 확률변수 X는 사건이 처음 발생하는 시간,공간이 되며, θ는 다음 사건이 발생하는 시간적, 공간적 평균길이 일때 X의 pdf는 모수 θ>0에 대해 f(x)=1θe−x/θ,0≤x<∞ 지수분포의 평균과 분산은 $$\begin{align*} \mu&=\t..
 연속형 확률분포 - 연속형 확률변수(Continuous Random Variables of The Continuous Type )
연속형 확률분포 - 연속형 확률변수(Continuous Random Variables of The Continuous Type )
연속형 확률분포(Continuous Distribution)-연속형 확률변수(Continuous Random Variables of The Continuous Type ) 구간 혹은 구간들의 합인 공간 S를 가지는 연속형 확률변수 X의 pdf는 다음의 조건을 만족하는 적분 가능한함수 f(x)이다. (a) f(x)>0,x∈S (b) ∫Sf(x)dx=1 (c) (a,b)⊆S 이라면 사상$\{a
 이산형 확률분포(Discrete Distribution) - 포아송분포(Poisson Distribution)
이산형 확률분포(Discrete Distribution) - 포아송분포(Poisson Distribution)
모수(population parameter) 모집단의 특성을 나타내는 수치이다. 포아송 분포에서 모수의 예는 9시에서 10시 사이에 교환대에 울리는 발신음의 수, 100feet 길이의 전선줄에 앉아있는 새의 수, 정오 12시에서 오후 2시까지 매표소에 도착하는 고객의 수, 어떤책의 한페이지에 나타난 오타의 수 등이 있다. 즉, 포아송 분포에서의 모수는 '단위시간 또는 단위공간에서 평균 발생 횟수' 이다. 포아송분포에서 모수는 수학기호 λ로 표시한다. 포아송분포(Poisson Distribution) 포아송분포는 단위시간, 단위공간 안에 어떤사건이 발생하는 평균 횟수 λ가 주어질 경우 사건이 발생하는 횟수를 확률변수 x로 두었을때의 이산 확률 분포이다. 주어진 연속구간에서 ..
 이산형 확률분포(Discrete Distribution) - 음이항분포(negative binomial distribution)
이산형 확률분포(Discrete Distribution) - 음이항분포(negative binomial distribution)
음이항분포는 베르누이 시행을 미리정한 성공횟수 r회가 될때까지 반복 시행할때 확률변수 X가 나타내는 분포를 말한다. pmf는 아래와 같다. g(x)=x−1Cr−1pr(1−p)x−r=x−1Cr−1prqx−r,x=r,r+1⋯ 음이항분포는 n번의 시행(여러번의 베르누이 독립시행)에서 n−1번의 실패에 대한 확률을 구하는 것이다. 베르누이 시행을 독립으로 반복하는 확률실험에서 X를 r회 성공하는데 필요한 시행 횟수라 하면, 확률의 곱셈법칙에 의해 X의 pmf g(x)는 x−1번째의 시행까지에서 정확하게 r−1회 성공할 확률 $${}_{x-1}C_{r-1}p^{r-1}(1-p)^{x-r}=_{x-1..
 이항분포표(Binomial Distribution Table)
이항분포표(Binomial Distribution Table)
https://www.statisticshowto.com/tables/binomial-distribution-table/#100
 이산형 확률분포(Discrete Distribution)- 이항분포(The Binomial Distribution)
이산형 확률분포(Discrete Distribution)- 이항분포(The Binomial Distribution)
어떤 사건들이 베르누이 시행으로 n번 발생되며 성공확률이 p일 경우 확률 변수 x를 성공 횟수로 두면 x는 이항분포를 따르며 아래의 개념들이 성립한다. f(x)=nCxpx(1−p)n−x μ=np σ2=npq 베르누이 실험(bernoulli experiment) ∘ 실험의 결과가 상호배타적이고 전체를 포괄하는 두 결과중 하나로 나타내는 확률실험 ex) 하나의 동전을 던져 앞면과 뒷면을 관찰하는 실험, 남⋅여로 구별되는 신생아의 성별, 양⋅부량 으로 판정되는 품질검사 ∘성공확률을 p, 실패확률을 q로 두면 q=1−p이고 베르누이 실험이 시행때마다 성공의 확률 p가 같..
 이산형 확률분포(Discrete Distribution)- 특별한 수학적 기댓값
이산형 확률분포(Discrete Distribution)- 특별한 수학적 기댓값
∘확률변수 X가 공간 S={u1,u2,⋯,ut} 에서 pmf f(x)를 갖고, 각각의 확률이 P(X=ui)=f(ui)>0 이고 ∑x∈Sf(x)=1 일때 확률변수 X의 평균(mean)은 아래와 같다. μ=∑x∈Sxf(x)=u1f(u1)+u2f(u2)+⋯ukf(uk) 적률(moment) 확률변수 X의 pmf가 f(x)일 때 a에 관한 시스템의 n차 적률은 아래와 같다. ∑x∈S(x−a)nf(x) X의 평균은 원점에 대한 1차적률이다. ∑x∈Sxf(x) 평균에 관한 2..
 이산형 확률분포(Discrete Distribution)- 확률변수, 수학적 기댓값
이산형 확률분포(Discrete Distribution)- 확률변수, 수학적 기댓값
확률 변수(Random Variable) ∙ 표본 공간 S를 갖는 확률 실험이 주어질때, 각 원소 s∈S에 대해 오직 하나의 실수 X(s)=x를 대응시키는 함수 X를 확률 변수라 한다. 즉, 어떤 사건, 사상에 수치가 부여된 함수라고 볼 수 있다. ∙ X의 공간(space)는 실수의 집합 {x:X(s)=x,s∈S}이다. ∙ 표본공간 S가 수가 아닐때에 S의 기술을 편리하게 해준다 ∙ 표본공간 S의 원소가 실수일 경우 X(s)=s이다. 그래서 X는 항등함수이고 X의 공간은 S이다. 한마리의 실험용 쥐를 무작위로 무리에서 꺼내 쥐의 성을 관찰하는 확률 실험에서 표본공간은 $S=\{female,m..

