이산형 확률분포(Discrete Distribution) - 포아송분포(Poisson Distribution)

모수(population parameter)

모집단의 특성을 나타내는 수치이다.

포아송 분포에서 모수의 예는 9시에서 10시 사이에 교환대에 울리는 발신음의 수, 100feet 길이의 전선줄에 앉아있는 새의 수, 정오 12시에서 오후 2시까지 매표소에 도착하는 고객의 수, 어떤책의 한페이지에 나타난 오타의 수 등이 있다.

즉, 포아송 분포에서의 모수는 '단위시간 또는 단위공간에서 평균 발생 횟수' 이다.

포아송분포에서 모수는 수학기호 $\lambda$로 표시한다.

 

포아송분포(Poisson Distribution)

포아송분포는 단위시간, 단위공간 안에 어떤사건이 발생하는 평균 횟수 $\lambda$가 주어질 경우 사건이 발생하는 횟수를 확률변수 $x$로 두었을때의 이산 확률 분포이다.

주어진 연속구간에서 발생하는 사건의 수가 다음의 조건을 만족시킨다면 모수 $\lambda>0$을 갖는 근사 포아송과정(approximate poisson process)을 따른다.

(a) 독립성 : 겹치치 않는 부 구간에서 발생하는 사건의 수들은 독립이다.
(b) 일정성 : 구간의 길이가 $h$인 충분히 짧은 길이의 구간(단위시간, 단위구간)에서 정확히 하나의 사건이 발생할 확률은 거의 $\lambda h$이다.
(c) 비집락성 : 충분히 짧은 길이의 구간에서 사건이 두 번 이상의 결과가 동시에 발생할 확률은 거의 0이다.

이때 단위길이가 1인 포아송분포의 $pmf$와 평균, 분산.
$$f(x)=\frac{\lambda^xe^{-\lambda}}{x!},\;\;\;\;x=0,1,2,\cdots,\;\;\;\lambda>0$$
$$\mu=\sigma^2=\lambda$$

단위길이가 $w$인 포아송분포의 $pmf$와 평균, 분산(평균과 분산에 수정 필요)
$$f(x)=\frac{(\lambda w)^xe^{-\lambda w}}{x!},\;\;\;\;x=0,1,2,\cdots,\;\;\;\lambda>0$$
$$\mu=\lambda e^{\lambda(1-w)}$$
$$\sigma^2=\lambda e^{\lambda(1-w)}+\lambda^2e^{\lambda(1-w)}-\lambda^2e^{2(1-w)}$$

위 조건을 간단한 예와 함께 확인하겠다.

(a) 독립성 : 아침 9시에서 아침 10시까지 국민은행에 방문한 고객의 수와 같은시간에 신한은행에 방문한 고객의 수는 독립이고, 아침 10시에서 11시사이에 신한은행에 방문한 고객의 수 또한 독립이다.

(b) 일정성 : 만약 어떤사건이 1분에 평균 2번 발생한다면 3분동안에는 평균 6번 발생한다는 것이다.

(c) 비집락성 : 서해안고속도로에서 같은시간에 같은지점에서 교통사고가 두번이상 발생할 확률은 무시해도 좋다.

 

이제 위 세가지 조건을 만족시키는 확률실험을 다루어보자.

$X$는 길이 1인 구간에서 발생하는 사건의 수라 한다.

이 실험에서 확률 $P(X=x)$($x$는 음이 아닌 정수)에 대한 근사확률을 구하기 위해서 길이 $1$인 구간을 $n$개로 나누어 길이가 $1/n$인 똑같은 길이의 부구간들을 만든다.

$n$이 충분히 크다면(즉, $x$보다 훨씬 크다면) 이 $n$개의 부 구간들 중 정확히 $x$개의 구간에서 사건이 각 한 번 발생할 확률이 구하고자 하는 근사확률이다.

길이 $1/n$인 어느 하나의 부 구간에서 사건이 한 번 발생할 확률은 조건 (b)에 의해서 근사적으로 $\lambda(1/n)$이다.

어느 하나의 부 구간에서 두번이상 사건이 발생할 확률은 조건 (c)에 의해서 0이다.

따라서 각 부 구간에서 정확히 한 번의 사건이 발생할 확률은 근사적으로 $\lambda (1/n)$ dlek.

각 부구간에서 사건이 발생 혹은 발생하지 않음은 베르누이 실험으로 생각할 수 있고, 조건 (a)에 의해서 성공의 확률 $p$가 대략 $\lambda (1/n)$인 베르누이 시행을 $n$회 행하는 실험에서 $X$는 사건의 발생횟수와 같다. 따라서 $P(X=x)$에 대한 근삿값은 이항확률

$${}_{n}C_{x}\left(\frac{\lambda}{n}\right)^x\left(1-\frac{\lambda}{n}\right)^{n-x}$$

에 의해 주어진다. $n$이 무한대로 증가하면

$$\begin{align*}
\lim_{n\rightarrow \infty} {}_{n}C_{x}\left(\frac{\lambda}{n}\right)^x\left(1-\frac{\lambda}{n}\right)^{n-x} &=\lim_{n\rightarrow\infty}\frac{n!}{x!(n-x)!} \left(\frac{\lambda}{n}\right)^x\left(1-\frac{\lambda}{n}\right)^{n-x}\\
&=\lim_{n\rightarrow\infty}\frac{n(n-1)\cdots(n-x+1)}{n^x}\frac{\lambda^x}{x!}\left(1-\frac{\lambda}{n}\right)^n\left(1-\frac{\lambda}{n}\right)^{-x}
\end{align*}$$

이제, 고정된 x에 대해

$$\lim_{n\rightarrow\infty}\frac{n(n-1)\cdots(n-x+1)}{n^x}=\lim_{n\rightarrow\infty}\left[(1)\left(1-\frac1 n\right)\cdots\left(1- \frac{x-1}{n}\right)\right]=1,\\
\lim_{n\rightarrow\infty}\left(1-\frac \lambda n\right)^n=e^{-\lambda},\\
\lim_{n\rightarrow\infty}\left(1-\frac \lambda n\right)^{-x}=1.$$

따라서

$$\lim_{n\rightarrow\infty}{}_{n}C_{x} \left(\frac{\lambda}{n}\right)^x\left(1-\frac{\lambda}{n}\right)^{n-x}=\frac{\lambda ^xe^{-\lambda}}{x!}=P(X=x)$$

를 얻을 수 있다. 위와같은 과정을 통해 확률분포인 포아송 분포의 pmf는 다음과 같이 주어진다.

$$f(x)=\frac{\lambda^xe^{-\lambda}}{x!},\;\;\;\;x=0,1,2,\cdots,\;\;\;\lambda>0$$

포아송 분포의 $pmf$의 총합이 1이 됨을 확인하자.

명백하게 $f(x) \geq 0$이고, $e^\lambda$의 맥로우린 급수 전개를 이용하면

$$\sum_{x=0}^{\infty}\frac{\lambda^xe^{-\lambda}}{x!}=e^{-\lambda}\sum_{x=0}^{\infty}\frac{\lambda^x}{x!}=e^{-\lambda}e^\lambda=1$$

$f(x)$는 $pmf$조건을 만족시킴을 확인하였다.

 

이제 포아송분포의 평균과 분산을 확인하겠다.

포아송 확률변수 $X$의 $mgf$는

$$M(t)=E(e^{tX})=\sum_{x=0}^{\infty}e^{tx}\frac{\lambda^xe^{-\lambda}}{x!}=e^{-\lambda}\sum_{x=0}^{\infty}\frac{(\lambda e^t)^x}{x!}$$

이다. 지수함수의 급수표현식을 이용하면 모든 실수 t에 대하여 아래 식을 갖는다.

$$M(t)=e^{-\lambda}e^{\lambda e^t}=e^{\lambda(e^t-1)}$$

이제 $mgf$의 처음 두 도함수는

$$M'(t)=\lambda e^te^{\lambda(e^t-1)}\\
M''(t)=(\lambda e^t)^2e^{\lambda(e^t-1)}+\lambda e^te^{\lambda(e^t-1)}$$

 

이를 이용하여 $X$의 평균과 분산을 구하면

$$\mu=M'(0)=\lambda,\\
\sigma^2=M''(0)-[M'(0)]^2=(\lambda^2+\lambda)-\lambda^2$$

즉, 포아송분포에 대해서

$$\mu=\sigma^2=\lambda$$

 

$$f(x)=\dfrac{(\lambda w)^x e^{-\lambda w}}{x!}$$

위 pdf의  mgf는

$$M(t)=E(e^{tx})=\sum_{x=0}^\infty e^{tx}f(x)=\sum_{x=0}^\infty e^{tx}f(x)=\sum_{x=0}^\infty e^{tx}\dfrac{(\lambda w)^x e^{-\lambda w}}{x!}=e^{-\lambda w}\sum_{x=0}^\infty \dfrac{(\lambda w)^x e^{tx}}{x!}$$

$$\begin{align*} 
&M(t)=e^{-\lambda w}e^{\lambda w e^t}=e^{\lambda w(e^t-w)}\\\\ 
&M'(t)=\lambda w e^t e^{\lambda w(e^t-w)}\\ 
&M'(0)=\lambda w e^{(1-w)}\\\\ 
&M''(t)=\lambda w e^t e^{\lambda(e^t-w)}+(\lambda w  
e^t)^2e^{\lambda(e^t-w)}\\ 
&M''(0)=\lambda w e^{\lambda(1-w)}+\lambda^2 e^{(1-w)}\\\\ 
&\mu=M'(0)=\lambda e^{(1-w)}\\ 
&\sigma^2=M''(0)-[M'(0)]^2=\lambda e^{\lambda(1-w)}+\lambda^2 e^{\lambda(1-w)}-\lambda^2e^{2(1-w)} 
\end{align*} $$

 

참고

다음은 $mgf$를 사용하지 않고 포아송분포의 평균과 분산을 구하는 방법을 살펴 보겠다.

평균을 구하는 방법은 아래와 같음을 기억하라

$$E(X)=\sum_{x\in S}xf(x)$$

$(0)f(0)=0$이고 $x>0$일 때 $\displaystyle \frac{x}{x!}=\frac{1}{(x-1)!}$이기 때문에 포아송분포의 평균은

$$E(X)=\sum_{x=0}^{\infty}x\frac{\lambda ^xe^{-\lambda }}{x!}=e^{-\lambda }\sum_{x=1}^{\infty}\frac{\lambda ^x}{(x-1)!}$$

이고, $k=x-1$이라 놓으면

$$E(X)=e^{-\lambda }\sum_{k=0}^{\infty}\frac{\lambda ^{k+1}}{k!}=\lambda e^{-\lambda }\sum_{k=0}^{\infty}\frac{\lambda ^k}{k!}=\lambda e^{-\lambda }e^\lambda =\lambda $$

 

분산의 계산을 위해 2차계승적률 E[X(X-1)]을 계산한다. $0(0-1)f(0)=0, (1)(1-1)f(1)=0,$ 그리고 $x>1$일 때 $\displaystyle \frac{x(x-1)}{x!}=\frac{1}{(x-2)!}$임을 이용하면

$$E[X(X-1)]=\sum_{x=0}^{\infty}x(x-1)\frac{\lambda^xe^{-\lambda}}{x!}=e^{-\lambda}\sum_{x=2}^{\infty}\frac{\lambda^x}{(x-2)!}$$

여기서 $k=x-1$이라 놓으면

$$E[X(X-1)]=e^{-\lambda}\sum_{k=0}^{\infty}\frac{\lambda^{k+2}}{k!}=\lambda^2e^{-\lambda}\sum_{k=0}^{\infty}\frac{\lambda^k}{k!}=\lambda^2e^{-\lambda}e^{\lambda}=\lambda^2$$

따라서

$$Var(X)=E(X^2)-[E(X)]^2=E[X(X-1)]+E(X)-[E(X)]^2=\lambda^2 + \lambda-\lambda^2=\lambda$$

$\blacksquare$

위 그림은 포아송분포에서 모수 $\lambda$가 $pmf$에 미치는 영향을 보여준다. 4개의 각각 다른 $\lambda$값에 대해 확률 히스토그램이 나타나 있다.

포아송과정에서 사건이 단위구간당 $\lambda$의 평균 비율로 발생한다면 구간길이 $t$에서 사건의 기대 발생건수는 $\lambda t$이다.

예를들어 $X$는 1초 동안 바륨-133에서 방사되는 알파 소립자의 수로서 가이거계수기에 의해 측정된다. 방사되는 소립자의 개수가 초당 60개의 평균비율로 발생한다면 1초의 1/10 동안 방사되는 소립자 수의 기댓값은 60(1/10)=6 이다. 게다가 길이 $t$의 시간 구간에서 방사되는 알파 소립자 수를 나타내는 $X$는 포아송 $pmf$

$$f(x)=\frac{(\lambda t)^xe^{-\lambda t}}{x!}, \;\;\; x=0,1,2,\cdots$$

를 갖는다. 이것은 길이 $t$의 구간을 마치 $\lambda$대신 평균 $\lambda t$를 가지는 단위구간처럼 처리하는 것이다.

$\blacksquare$

 

독립성과 집락성, 비일정성이 만족되도록 매우 큰 $n$과 작은 $p$에 대해 $X$가 이항분포 $b(n,p)$를 갖는다면 $X$는 포아송분포를 따른다.
즉, 이항분포는 포아송 분포로 근사화 시킬 수 있다.
$$f(x)=\frac{(np)^xe^{-np}}{x!} \approx {}_nC_{x}p^x\left(1-p\right)^{n-x}$$

이항분포의 평균 $\mu = np$ 임을 생각하면 좌변의 식을 이해 할 수 있다.

 

포아송분포에서 $n$이 굉장히 크다면 이항분포에 대한 근사확률을 구하는데 사용가능하다.

$X$가 모수 $\lambda$를 갖는 포아송분포를 가진다면 굉장히 큰 $n$에 대해서

$$P(X=x)\approx {}_nC_{x}\left(\frac{\lambda}{n}\right)^x\left(1-\frac{\lambda}{n}\right)^{n-x}$$

임을 알고 있다. 위의 이산확률에서 $p=\lambda / n$은 $\lambda=np$로 표현이 가능하다.

따라서

$$\frac{(np)^xe^{-np}}{x!}\approx nC_{x}p^x\left(1-p\right)^{n-x}$$

이때 $\lambda$는 고정된 상수이고 $np=\lambda$이므로 $p$는 작아야 한다.

가령 $n \geq 20$이고 $p \leq 0.05$ 혹은 $n \geq 100$이고 $p \leq 0.1$ 일때 매우 정확하다.

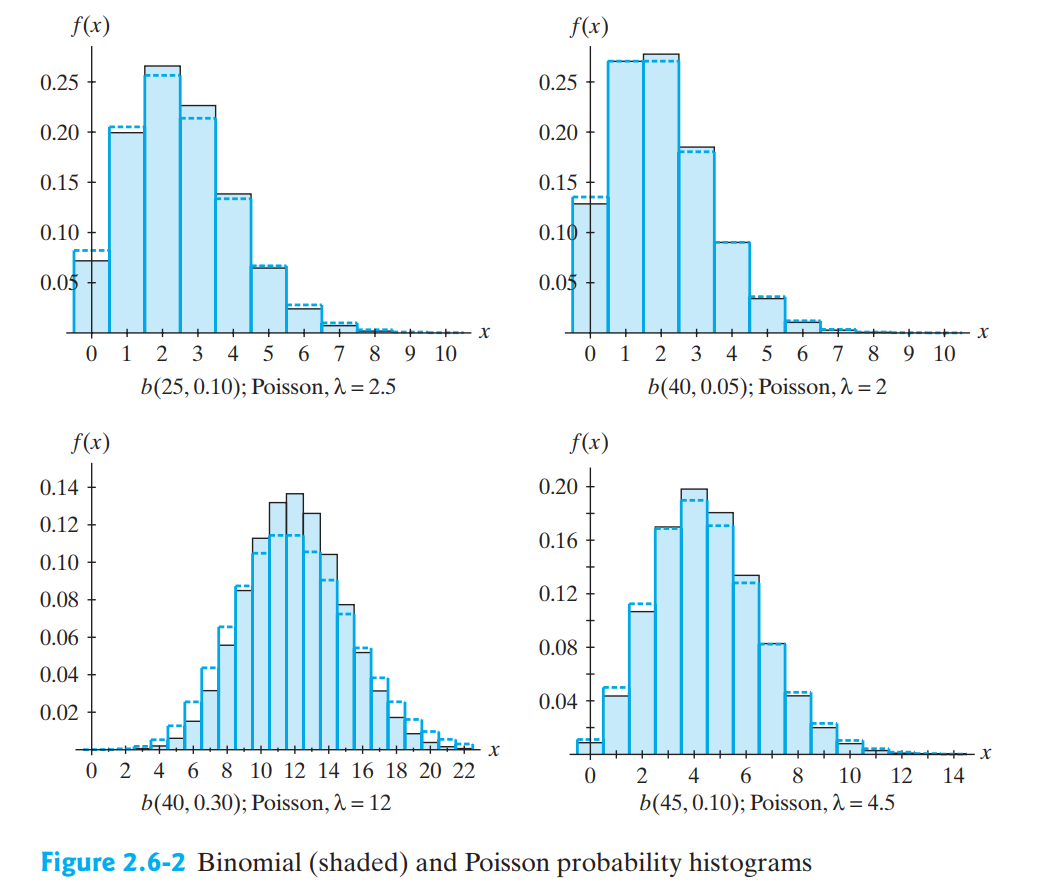
위 그림에서 음영표시된 이항분포 $b(n,p)$의 확률히스토그램과 $\lambda = np$를 갖는 포아송분포로 근사시켰을 대의 확률 히스토그램이 보여진다.

$p$가 클때($p=0.3$에서) 근사확률은 정확한 확률과 차이가 난다.

 

포아송분포표를 확인하여 여러 $\lambda$값에 대한 포아송 $cdf$의 값들을 확인할 수 있다.

예제 2.6-1의 경우 

$\displaystyle f(x)=\dfrac{\lambda^x e^{-\lambda}}{x!}$

그러므로

$f(6)=\dfrac{5^6 e^{-5}}{6!}=0.1462$