| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 스토어드 프로시저
- two pointer
- binary search
- 다익스트라
- Stored Procedure
- String
- Two Points
- Brute Force
- Dijkstra
- Hash
- SQL
- union find
- DP
- MYSQL
- 그래프
- 이진탐색
- Trie
- Today
- Total
codingfarm
이산형 이변량 분포(Bivariate Distribution of The Discrete Type) 본문
이산형 이변량 분포(Bivariate Distribution of The Discrete Type)
$\bullet$ 두개 이상의 확률변수에 대한 분포에 대해 다뤄본다
ex) 대학 입시에서 내신성적 $X$와 수능성적 $Y$의 관계 $\rightarrow$ 대학교성적 $Z$의 예측 가능 여부 확인
초등학생의 키(X), 몸무게(Y), 발사이즈(Z)간의 관계 $\rightarrow$ 성인이 됐을때의 키 $W$ 예측 가능한가?
$X,Y$를 이산형 확률 공간에서 정의된 두개의 확률 변수라 하고 $X$와 $Y$에 대응하는 2차원 공간을 $S$라 하자. $X=x, ~Y=y$인 확률을
$f(x,y) = P(X=x, Y=y)$
라 하면, $f(x,y)$는 $X$와 $Y$의 결합확률질량함수(joint probability mass function; joint pmf)라 하고 다음과 같은 성질을 가진다.
(a) $0 \leq f(x,y) \leq 1$
(b) $\displaystyle \underset{(x,y) \in S}{\sum \sum} f(x,y) = 1$
(c) $\displaystyle P[(X,Y) \in A] = \underset{(x,y) \in A}{\sum \sum}f(x,y)$, 여기서 $A$는 공간 $S$의 부분집합이다.
예를 통해 개념을 확인해보자
주사위를 2번 던진다. 그러면 확률 $1/36$을 갖는 $36$개의 실현치에 대해서 보다 작은 수를 $X$, 보다 큰수를 $Y$라 하면 결합 $pmf$는 다음과 같다.
$$f(x,y) = \begin{cases} 1 / 36 & 1 \leq x = y \leq 6 \\ 2/36 & 1 \leq x < y \leq 6 \end{cases}$$
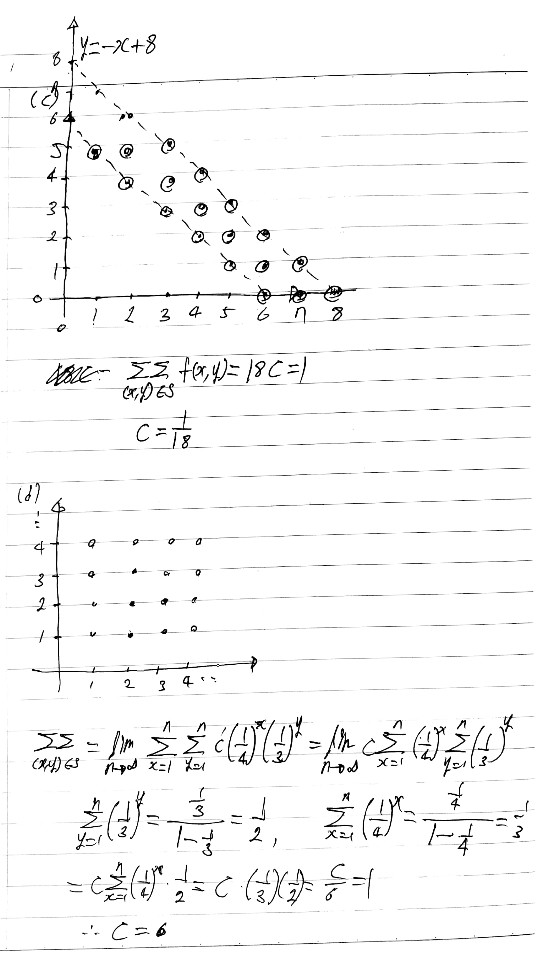
아래 그림은 공간 $S$의 여러 실현치에 대한 확률을 보여준다

위 그림은 두개의 주사위를 던젔을때 나온눈에 대한 확률을 보여준다
각 아래쪽과 왼쪽에 적힌 확률은 행확률들과 열확률들의 합이다.
각 열확률들의 합은 $X$가 $x$공간 $S_x = \{ 1,2,3,4,5,6 \}$의 값을 취할때의 확률이고
각 행확률들의 합은 $Y$가 $y$공간 $S_y = \{ 1,2,3,4,5,6 \}$의 값을 취할때의 확률이다.
각 확률들의 합은 $X$와 $Y$의 $pmf$를 나타낸다.
이러한 확률들은 흔히 확률분포표의 주변에 기록되기에 주변확률질량함수(marginal pmf)라 한다.
$X,Y$가 공간 $S$에서 결합 $pmf$ $f(x,y)$를 가질때 $X$만의 $pmf$ 또는 $Y$만의 $pmf$를 각각 $X$ 또는 $Y$의 주변확률질량함수(marginal probability mass function)라 하고 아래처럼 정의된다.
$$f_X(x) = \underset{y}{\sum} f(x,y)=P(X=x);~~~~x \in S_X\\ f_Y(y) = \underset{x}{\sum} f(x,y)=P(Y=y);~~~~y \in S_Y$$
그리고 확률변수 $X,Y$가
$f(x,y) = f_X(x) \cdot f_Y(y)$ 모든 $x \in S_X$, 모든 $y \in S_Y$일때, 그때에 한해서 $X,Y$는 독립(independent)라 하고 그렇지 않으면 $X,Y$는 종속(dependent)라 한다.
2개의 주사위를 던지는 상황에서는 많은 경우에 $f(x,y) \neq f(x) f(Y)$이다.
가령
$f(X=3,Y=3) = 1/36\\ f(X=3) = 7/36 \\ f(Y=3) = 5/36\\
f(X=3,Y=3) \neq f(X=3) \cdot f(Y=3)$
그러므로 $X$와 $Y$는 종속이다.
두 확률변수를 $X_1, X_2$라 하자
$X_1, X_2$를 공간 $S$상에서 결합 $pmf$ $f(x_1,x_2)$를 갖는 이산형 확률변수 라 하자
$u(x_1,x_2)$를 두 확률변수에 대한 함수이면
$$E[u(X_1, X_2)]= \underset{(x_1, x_2 \in S)}{\sum \sum}u(x_1, x_2)f(x_1,x_2)$$
를 $u(X_1, x_2)$의 수학적기댓값(mathematical expectation, expected value)라 한다.
여기서
$$\underset{(x_1, x_2 \in S)}{\sum \sum} \left| u(x_1, x_2) \right| f(x_1,x_2)$$
는 유한의 값을 가지며 수렴한다 가정한다.
그리고 $Y = u(X_1, X_2)$가 공간 $S_Y$상에서 $pmf~g(Y)$를 갖는 확률변수이면
$$\underset{(x_1, x_2 \in S)}{\sum \sum} u(x_1, x_2) f(x_1,x_2) = \sum_{y \in S_Y}y~g(y)$$
도 성립한다.
다음과 같은 수학적 기댓값은 그것이 존재할때 특별한 명칭을 갖는다.
1) $u_i(X_1, X_2) = X_i, ~~~ i=1,2$ 이면
$$E[u_i(X_1, X_2)]=E(X_i) = \mu_i$$
는 $X_i$, $i=1,2$의 평균(mean)이라 한다.
2) 만일 $u_i(X_1, X_2) = (X_i - \mu_i)^2.~~i=1,2$ 이면
$$E[u_i(X_1, X_2)]=E[(X_i - \mu_i)^2]=\sigma_i^2 = Var(X_i)$$
는 $X_i$, $i=1,2$의 분산(variance)라 한다.
우리는 확률변수가 2개인 경우의 분포에서는 공간 $S$가 직사강형을 이루고, 결합함수가 각 확률변수들의 곱으로 되어있으면 독립임을 알 수 있다. 이는 확률변수가 다수로 이루어젔을때에 대해서도 일반화 가능하다. 대표적으로 2개의 주사위를 던지는 경우와 예제 4.1-4의 경우에 공간 $S$는 삼각형을 이루므로 종속이 되고 예제 4.1-3의 공간 $S$가 직사강형이고 결합함수가 확률변수의 곱으로 되어있으며 독립임에 주목하라
'통계학 > 수리통계학' 카테고리의 다른 글
| 4.3 조건부 분포(Conditional Distribution) (0) | 2020.09.01 |
|---|---|
| 피어슨 상관 계수(Pearson Correlation Coefficient) (0) | 2020.08.14 |
| 정규 분포(Normal Distribution) (0) | 2020.06.24 |
| 연속형 확률분포 - 카이제곱분포(chi-square distribution) (0) | 2020.04.30 |
| 연속형 확률분포 - 감마분포(The Gamma Distributions) (0) | 2020.04.23 |