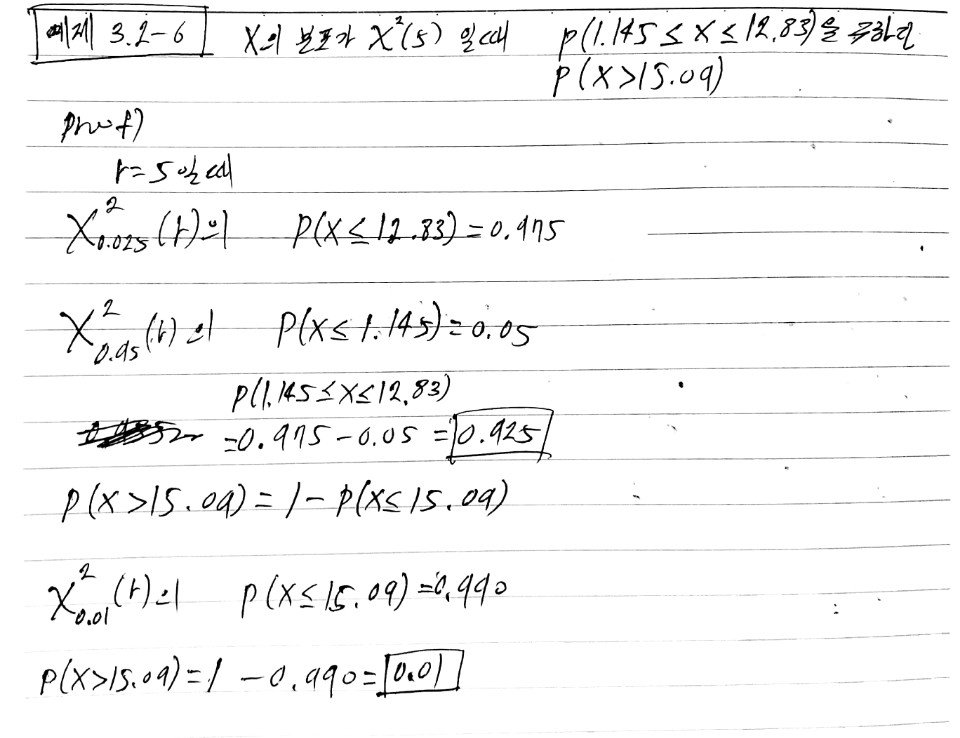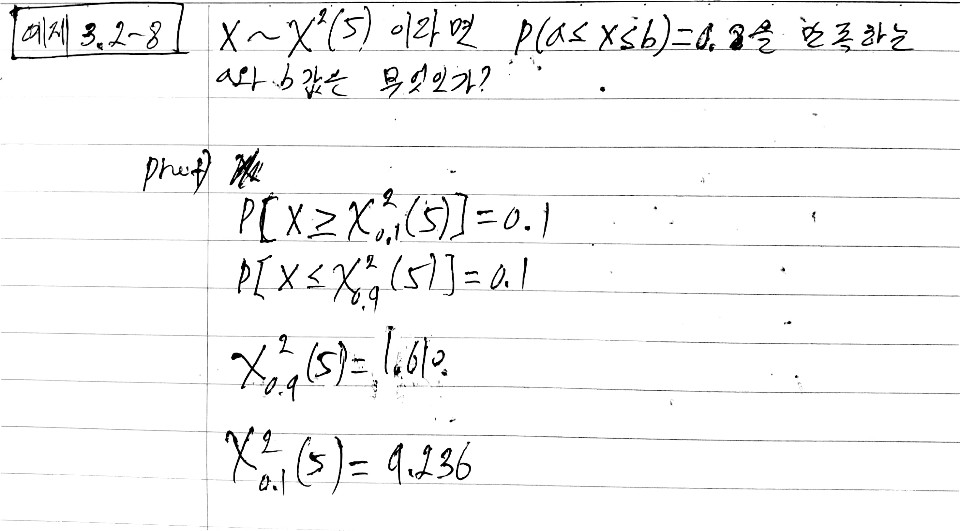| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- MYSQL
- Brute Force
- Trie
- 이진탐색
- two pointer
- union find
- String
- Stored Procedure
- 스토어드 프로시저
- DP
- binary search
- SQL
- 다익스트라
- Dijkstra
- Hash
- Two Points
- 그래프
Archives
- Today
- Total
codingfarm
연속형 확률분포 - 카이제곱분포(chi-square distribution) 본문
카이제곱 분포는 감마분포에서 $\theta=2,\;\;\alpha=\dfrac{r}{2}\;(r\;is\;positive\;integer)$을 가지는 특수한 분포를 가리킨다.
확률변수 $X$의 $pdf$는
$$f(x)=\frac{1}{\Gamma(r/2)2^{r/2}}x^{(r/2)-1}e^{-x/2}\;\;\;\;,0 < x < \infty$$
$X$는 자유도(degree of freedom) $r$의 카이제곱분포를 따른다 하고 $\chi^2(r)$이라 표기한다.
평균과 분산
$$\mu=r\;\;\;\;\;,\sigma^2=\alpha \theta^2=2r$$
자유도 $r$과 $x$값에 대한 카이제곱 $cdf$
$$F(x)= \int_{0}^{x} \frac{1}{\Gamma(r/2)2^{r/2}}w^{(r/2)-1}e^{-w/2}\;dw$$
카이제곱의 $mgf$
$M(t)=(1-2t)^{-r/2}\;\;\;\;\;,t<\dfrac{1}{2}$
이며 이를통해 평균과 분산을 구할 수 있다.
$$\mu=\alpha\theta=\frac{r}{2}2=r\;\;\;\;\;,\sigma^2=\alpha \theta^2=\frac{r}{2}2^2=2r$$
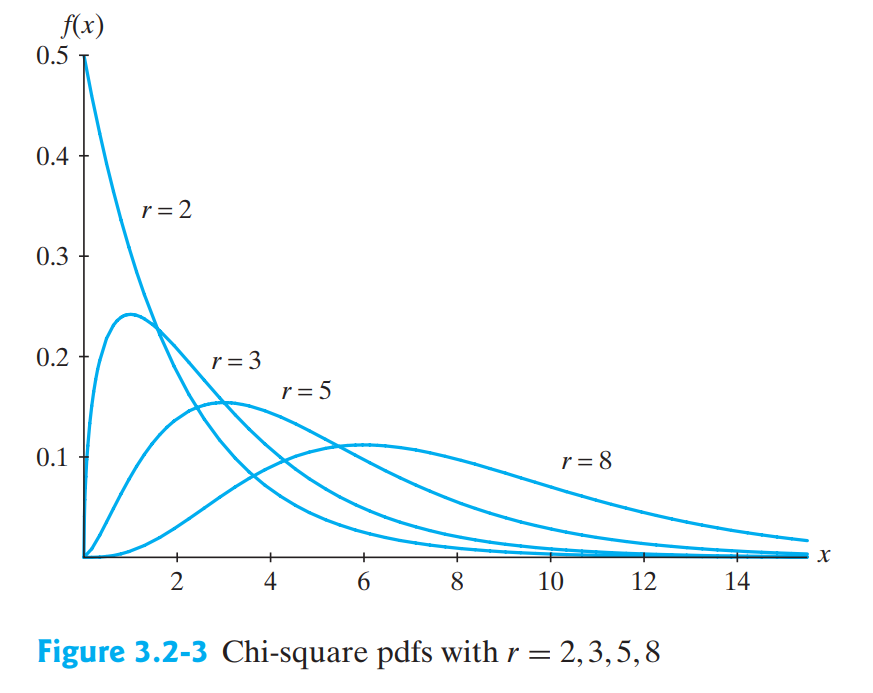
자유도 $r$과 $x$값에 대한 카이제곱 $cdf$
$$F(x)= \int_{0}^{x} \frac{1}{\Gamma(r/2)2^{r/2}}w^{(r/2)-1}e^{-w/2}\;dw$$
카이제곱분포는 응용분야에서 매우 중요하므로 미리 여러값들이 주어진다.



예제 3.2-7 에서의 확률들은 통계응용에서 매우 중요하다. 따라서 $a$와 $b$에 대해 특별한 표기를 사용한다.
$\alpha$를 양의 확률(보통 $0.5$보다 작은) 그리고 $X$는 $\chi^2(r)$분포를 가진다 하자.
그러면 다음과 같이 정의되는 $\chi^2(r)$분포의 백분위수는 통계응용에서 매우 유용하다. 즉 $\chi_\alpha^2(r)$은
$$P[X \geq \chi_\alpha^2(r)]=\alpha$$
를 만족하는 $\chi^2(r)$ 분포의 제$100(1-\alpha)$백분위수(혹은 상위 $100\alpha$백분위수)이고, $\chi_{1-\alpha}^2(r)$은
$$P[X \leq \chi_{1-\alpha}^2(r)]=\alpha$$
를 만족하는 $\chi^2(r)$ 분포의 제$100\alpha$백분위수이다.

'통계학 > 수리통계학' 카테고리의 다른 글
| 이산형 이변량 분포(Bivariate Distribution of The Discrete Type) (0) | 2020.07.01 |
|---|---|
| 정규 분포(Normal Distribution) (0) | 2020.06.24 |
| 연속형 확률분포 - 감마분포(The Gamma Distributions) (0) | 2020.04.23 |
| 연속형 확률분포 - 지수분포(The Exponential Distributions) (0) | 2020.04.21 |
| 연속형 확률분포 - 연속형 확률변수(Continuous Random Variables of The Continuous Type ) (0) | 2020.04.21 |
Comments