| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 다익스트라
- 그래프
- Two Points
- String
- Brute Force
- MYSQL
- 스토어드 프로시저
- Stored Procedure
- Trie
- Dijkstra
- Hash
- binary search
- union find
- two pointer
- SQL
- DP
- 이진탐색
- Today
- Total
codingfarm
3. 확률 분포 추정 - 최대 우도 추정(Maximum Likelihood Estimation) 본문
해당 블로그글들을 많이 참고하였다.
https://ratsgo.github.io/statistics/2017/09/23/MLE/
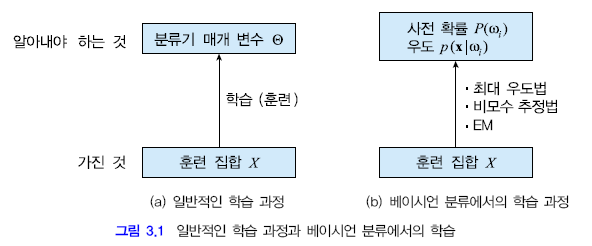
최대 우도 추정(ML estimation)
ML 방법
샘플집합 $X$가 주어질때 $X$를 발생시켰을 확률이 가장 높은 $\Theta$를 찾기 위해 $L(\Theta|X)$를 최대로 하는 $\Theta$를 찾는 방법이다.
베이즈 원리에 의해 $L(\Theta|X)$는 $P(X|\Theta)$에 비례하므로
$$\hat \Theta=\underset{\Theta} {\arg\max}\;P(X|\Theta) =\underset{\Theta} {\arg\max}\;P(X_1,X_2,\cdots,X_n|\Theta)$$
각 샘플이 독립적으로 추출되었다면
$$\hat \Theta=\underset{\Theta} {\arg\max}\;\sum_{i=1}^{N} \ln P(X_i|\Theta)$$
위의 최적화 문제를 해결하여 우도를 최대로 하는 $\Theta$를 찾는다.
추정하고자 하는 확률분포가 정규분포를 따른다면
$P(X)=N(\mu,\Sigma)$
$\displaystyle \mu=\dfrac{1}{N}\sum_{i=1}^{N}X_i$
MAP 방법
ML방법에서 $P(\Theta)$가 균일하지 않을 경우
$$\hat \Theta=\underset{\Theta} {\arg\max}\;P(\Theta) \sum_{i=1}^{N} \ln P(X_i|\Theta)$$
개념적으로는 어떠한 형태의 분포에도 적용이 가능하다.
풀어야 하는 제를 다음과 같이 정의 할 수 있다. "주어진 $X$를 발생시켰을 가능성이 가장 높은 $\Theta$를 찾아라."
관측치(obserber; $X = {x_1, x_2, ..., x_n}$)가 주어진 통계모델의 우도$L(\Theta|X)$를 최대화 하는 매개변수 $\Theta$를 찾는 과정이라 정의 한다.
우도$L(\Theta|X)$는 $\Theta$가 전제 되었을때 표본 $X$가 등장할 확률인 $P(X|\Theta)$에 비례한다.
즉, $P(X|\Theta)$를 최대로 하는 $\Theta$를 찾는게 최대 우도법이라 볼 수 있다.
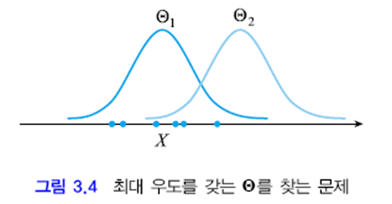
가령 그림3.4에서 $X$는 여섯개의 샘플을 갖는다. 이 $X$를 발생시킬 확률은 $\Theta_1$이 $\Theta_2$보다 더 높다. 즉, $\Theta_1$의 우도 $p(X|\Theta_1)$이 $\Theta_2$의 우도 $p(X|\Theta_2)$ 보다 더 높다고 할 수 있다.
어떤 $\Theta$가 최대 우도를 가질지를 추정하는것이 우리가 풀어야할 문제이다.
$\hat{\Theta} = \underset{\Theta}{argmax}P(X|\Theta)$ (1)
확률 분포 추정 문제를 (1)과 같이 최대 우도를 갖는 매개 변수를 찾는것으로 규정하고 해를 구하는 방법을 최대 우도 방법(maximum likelihood method; ML) 이라 한다.
주어진 입력을 통해 $P(X|\Theta)$는 아래와 같이 새로 정의 가능하다.
$P(X|\Theta) = P(X_1, X_2,\cdots ,X_n|\Theta)$
최대값을 찾는다는 점에서 최대 우도 추정은 최적화 문제(optimization problem)이다.
동전을 던진후에 나온 결과를 통해 동전의 앞면이 나올 확률을 추정하는 방법에 대한 예와 함께 최대 우도법을 실행하는 방법에 대해 알아보겠다.
100개의 동전을 던져서 56개가 앞면이 나오는 관찰(observation)을 하였다. 관측치 x를 앞면이 나온 횟수, 미지의 모수 혹은 매개변수 $\Theta$를 앞면이 나올 확률 $P$라 정의한다. 이제 관측된 결과를 통해 확률 $P$를 구해보자.
앞면이 나올 확률 P에 따라 X개의 동전이 앞면이 나올 확률은 아래와 같이 이항분포로 나타낼 수 있다.
$P(X=k|P)=_{n}\textrm{C}_{k}P^k(1-P)^{n-k}$
가령 앞면이 56개 나오고, P=0.5일때는
$P(X=k|P)=_{100}\textrm{C}_{56}(0.5)^{56}(0.5)^{44}=0.0389$
이제 우도를 최대로 하는 P값을 찾기위해 여러 값들을 넣어보면서 비교해보자
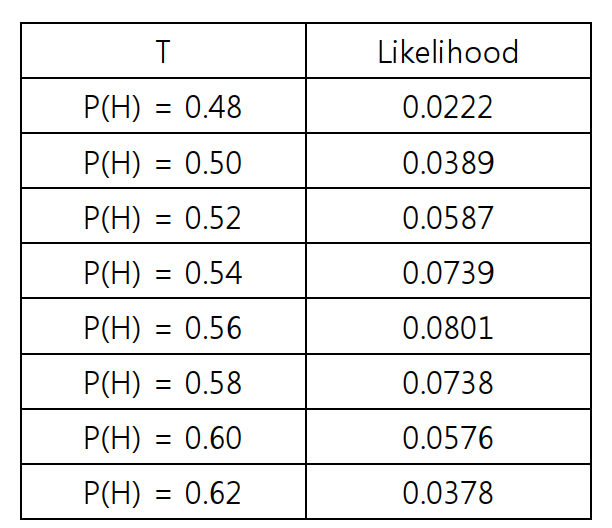
이것으로 우리는 동전 앞면이 나올 확률 P = 0.56이 됨을 알 수 있다.
모든 샘플이 독립적으로 추출되 i.i.d. ( independent and identical distributed ) 하다면 아래와 같이 표현 가능하다.
$P(X|\Theta)=P(x_1|\Theta)P(x_2|\Theta)\cdots P(x_N|\Theta)=\prod\limits_{i=1}^{N}P(x_i|\Theta)$ (2)
식(1)에 단조증가함수인 ln을 취하여 로그 우도(log likelihood)로 표현 할 수 있다.
식(1)에 식(2)를 대입하고 ln 함수를 취하여 로그 우도 형태로 다시 쓰면 아래 식을 얻는다.
$\hat{\Theta} = \underset{\Theta}{argmax}\sum\limits_{i=1}^{N} \ln P(X_i|\Theta)$ (3)
식(3)는 최적화 문제(optimization problem)이다. 이 문제를 어떻게 풀것인가? 여러가지 최적화 알고리즘이 있으며 이를 적용 가능하다 여기서는 가우시안이 하나이므로 미분을 이용한 풀이를 제시하겠다.
$$\begin{cases}
\dfrac{\partial L(\Theta)}{\partial \Theta}=0\\
이때\; \displaystyle L(\Theta)=\sum_{i=1}^{N}\ln p(x_i|\Theta)
\end{cases}$$
위식을 만족하는 해중에 $L(\Theta)$를 최대로 하는 해를 취한다.
$\blacksquare$
추정하고자 하는 확률 분포가 정규 분포를 따른다 가정하고 평균벡터$\mu$를 구하는 방법을 알아본다. 공분산행렬$\Sigma$는 이미 주어진다 가정하면 $\Theta=\{평균\;벡터\;\mu,공분산\;행렬\;\Sigma \}$ 이다. 즉 $p(X)=N(\mu,\Sigma)$이다. d는 특징 벡터 $x_i$의 차원이다. 이제 식 (3.5)에 정규분포 공식을 대입하고 정리하자.
$\displaystyle P(x_i|\Theta)=p(x_i|\mu)=\dfrac{1}{(2\pi)^{d/2}|\Sigma|^{1/2}}\exp \left( -\dfrac{1}{2}(x_i-\mu)^T\Sigma^{-1}(x_i-\mu) \right)\\
\displaystyle \ln p(x_i|\mu)=-\dfrac{1}{2}(x_i-\mu)^T\Sigma^{-1}(x_i-\mu)-\dfrac{d}{2} \ln 2\pi - \dfrac{1}{2}\ln |\Sigma|\\
\displaystyle L(\mu)=-\dfrac{1}{2}\sum_{i=1}^{N}(x_i-\mu)^T\Sigma^{-1}(x_i-\mu)-N \left(\dfrac{d}{2} \ln 2\pi + \dfrac{1}{2} \ln |\Sigma| \right)\\
\displaystyle \dfrac{\partial L(\mu)}{\partial \mu}=\sum_{i=1}^{N}\Sigma^{-1}(x_i-\mu)$
이제 $\dfrac{\partial L(\mu)}{\partial \mu}$를 $0$으로 두고 식을 정리하면
$$\sum_{i=1}^{N}\Sigma^{-1}(x_i-\mu)=0\\
\sum_{i=1}^{N}x_i-N\mu=0$$
위 식을 정리하여 아래식을 얻는다.
$$\hat \mu=\dfrac{1}{N}\sum_{i=1}^{N}x_i$$
샘플의 특징 벡터를 모두 더하고 그것을 $N$으로 나누어주면 평균벡터가 된다는 우리의 직관과 일치하는 식을 얻었다.
이때 까지 $p(\Theta)$가 균일하다는 가정이 깔려 있었다. 이제 균일하지 않다고 고려하고 식(3)을 아래처럼 고처쓰겠다.
$$\hat \Theta=\underset{\Theta}{\arg\max} \;p(\Theta)\sum_{i=1}^{N}\ln p(x_i|\Theta)$$
위 식을 풀어 최적의 매개변수를 찾는 방법을 MAP(maximum a posterior; 최대 사전확률)방법이라 한다.
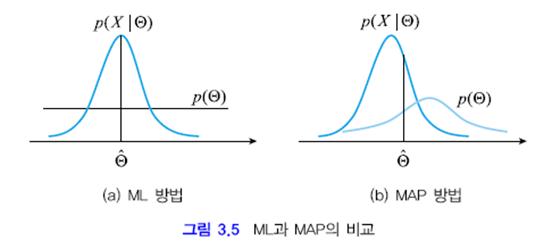
그림 3.5는 ML과 MAP을 비교한다. MAP에서는 사전확률이 균일하지 못해서 최적해에 영향을 끼침에 주목하라
'AI > 패턴인식' 카테고리의 다른 글
| 3. 확률 분포 추정 - 파젠창(Parzen Window) (0) | 2020.04.10 |
|---|---|
| 3. 확률 분포 추정 - 히스토그램 추정(histogram estimation) (0) | 2020.04.10 |
| 3. 확률 분포 추정-개요 (0) | 2020.04.09 |
| 2. 베이시언 결정 이론 (0) | 2020.01.29 |
| 1. 소개 (0) | 2020.01.28 |




