| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 이진탐색
- DP
- SQL
- union find
- Brute Force
- 다익스트라
- Hash
- two pointer
- Stored Procedure
- MYSQL
- Trie
- binary search
- Dijkstra
- Two Points
- String
- 그래프
- 스토어드 프로시저
- Today
- Total
codingfarm
3. 확률 분포 추정 - 파젠창(Parzen Window) 본문
$\circ$ 최대 우도 추정법에서 나온 ML과 MAP는 모수적(parametric) 방법이다.
$\circ$ 모수적 방법은 매개변수 $\Theta$ (모수)로 표현할 수 있는 특정한 종류의 확률분포에만 사용가능하다는 한계를 지녔다. 현실에서는 특정한 확률 분포를 안따르는 경우가 매우 많음.
$\circ$ 이 절에서는 확률 분포 추정을 위한 비모수적방법(nonparametric)으로 파젠창과 최근접이웃을 소개한다.
$\circ$ k-NN 분리기는 확률분포 추정을 위한 방법이 아니라 분류를 위한 방법이다. 하지만 동작 원리 측면에서는 최근접 이웃과 유사하다.
파젠 창(Parzen window)
$\circ$ 임의의 확률 분포에 적용 가능하다.
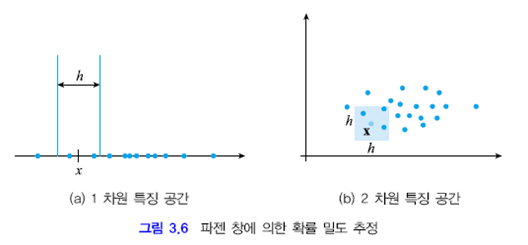
그림 3.6 (a)에서 임의의 점 $x$에서 확률값을 추정하고 싶다.
점 $x$를 중점으로 하는 크기 $h$인 창을 씌우고 이 창안에 있는 샘플의 개수를 세어 $k$라 한다. 그러면 확률은 $\displaystyle p(x)=\frac{1}{h} \frac{k}{N}$ 와 같이 추정할 수 있다.($N$ : 전체 샘플의 수)
2차원의 경우 $\displaystyle p(x)=\frac{1}{h^2} \frac{k}{N}$로 추정할 수 있다.
d차원의 경우 창의 부피는 $h^d$가 되므로 확률은 아래와 같다.
$\displaystyle p(x)=\frac{1}{h^d} \frac{k_x}{N}$
$x$는 $d$차원의 특징공간상의 점이다.
$h$와 $N$은 입력에 따라 무관하고 $k$만이 $x$에 의존적이므로 $k_x$라는 표기를 하였다.
파젠창과 히스토그램 추정의 차이가 무엇인가?
이제 연속된 공간에서 임의의점 $x$에 대해 확률 밀도 함수를 얻게 되었다.
$\circ$ 하지만 이런 방법은 불연속적인 확률값을 갖게된다. 가령 그림 3.6 (a)에서 $h$ 구간을 오른쪽으로 옮겨가다보면 샘플 하나가 영역내에 추가로되는순간 $k=2$에서 $k=3$으로 계단모양의 확률밀도함수가 만들어 진다.
$\circ$ 연속적인 확률 밀도 함수를 구하기 위해선 창안의 샘플에 각기 다른 가중치를 부여하는 것이다. 즉 $x$에 가까울수록 비중을 보다 크게두고 경계에 가까워진다면 0에 가까운 가중치를 가지게끔 하면 된다.
먼저 계단함수 형태의 커널함수에 대해 알아보자.
$$\kappa(x)=\begin{cases}1,& |x_i| \leq 0.5,& 1\leq i \leq d \\ 0, &otherwise\end{cases}$$
위 식은 창 내부 구간은 1을 갖고 그 이외의 구간은 0을 갖는 함수이다.

앞서 구했던 임의의 점 $x$에서의 확률값 추정 함수에서
$\displaystyle p(x)=\frac{1}{h^d} \frac{k_x}{N}$
$k_x$는 아래와 같이 고쳐 쓸 수 있다.
$\displaystyle k_x=\sum_{i=1}^{N}\kappa \left(\frac{\mathscr x - \mathscr x_i}{h}\right)$
$\displaystyle p(\mathscr x)=\frac{1}{h^d}\frac{1}{N}\sum_{i=1}^{N}\kappa\left(\frac{\mathscr x - \mathscr x_i}{h} \right)$
샘플 $\mathscr x_i$가 $\mathscr x$를 중심으로 하는 크기가 $h$인 창에서 존재하면 $\displaystyle \kappa \left(\frac{\mathscr x - \mathscr x_i}{h} \right)$는 1이 되고 아니면 0이 된다.
가령 $\mathscr x_i$가 경계에 있다면 $\displaystyle \mathscr x_i=x-\frac{h}{2}$이고 $\displaystyle \kappa \left( \frac{\mathscr x - \mathscr x_i}{h} \right)=1$ 이어야 한다.
이때 $\displaystyle \frac{\mathscr x-\mathscr x_i}{h}=\frac{\displaystyle \mathscr x - \mathscr x + \frac{h}{2}}{h}=\frac{1}{2}$ 로 경계값이 됨을 알수 있다.
커널함수가 계단함수 이므로
$\displaystyle p(\mathscr x)=\frac{1}{h^d}\frac{k_{\mathscr x}}{N}$과 $\displaystyle p(\mathscr x)=\frac{1}{h^d}\frac{1}{N}\sum_{i=1}^{N}\kappa\left(\frac{\mathscr x - \mathscr x_i}{h} \right)$ 는 같다.
$\circ$ 이제 커널함수를 그림 3.7 (b)와 같이 매끄러운(smooth) 함수로 대치하여 확률밀도함수가 연속적으로 되게끔 할 수 있다.
이때의 커널함수$\kappa(\mathscr x)$는 확률이므로 $\kappa(\mathscr x) \geq 0$ 과 $\displaystyle \int_{\mathscr x}\kappa(\mathscr x)d\mathscr x =1$를 만족해야 한다.
위 조건을 만족하는 대표적인것이 정규분포(가우시안 분포 or 가우시안 함수) 이다. 따라서 원점을 0으로 하고 단위행렬을 $I$를 공분산행렬로 갖는 가우시언 함수를 사용한다.
즉, $\kappa(\mathscr x)=N(0,I)$로 두고 $\displaystyle p(\mathscr x)=\frac{1}{h^d}\frac{1}{N}\sum_{i=1}^{N}\kappa\left(\frac{\mathscr x - \mathscr x_i}{h} \right)$ 을 계산한다.
벡터집합에 대한 정규분포식은 아래와 같다
$\displaystyle N(\mu, \Sigma)=\frac{1}{(2\pi)^{d/2}|\Sigma|^{1/2}}exp \left(-\frac{1}{2}(\mathscr x - \mu)^T\Sigma^{-1}(\mathscr x-\mu) \right)$
$\circ$ $N$이 충분히 크고 $h$가 충분히 작으면 파젠창 방법으로 추정한 $p(\mathscr x)$는 실제 확률 분포에 매우 가까워진다. 하지만 훈련집합의 갯수($N$)가 한정되 있을 경우 조정 가능한 수치는 $h$ 뿐이다. 그러므로 최적의 $h$값을 실험적으로 정하는 것이 현실적이다.
$\circ$ 파젠창방법 또한 차원의 저주에서 자유롭지 못한다 대략 1차원에서 $N_1$개의 샘플이 필요하면 d차원에서는 $N_1^d$개 만큼의 샘플이 필요하다.
$\therefore$ 파젠창은 낮은 차원에서만 사용가능하다.
'AI > 패턴인식' 카테고리의 다른 글
| 3. 확률 분포 추정 - 최근접 이웃 분류기(k-nearest neighbour(k-NN) classifier) (0) | 2020.04.11 |
|---|---|
| 3. 확률 분포 추정 - 최근접 이웃 추정(k-nearest neighbours estimation) (0) | 2020.04.11 |
| 3. 확률 분포 추정 - 히스토그램 추정(histogram estimation) (0) | 2020.04.10 |
| 3. 확률 분포 추정 - 최대 우도 추정(Maximum Likelihood Estimation) (0) | 2020.04.10 |
| 3. 확률 분포 추정-개요 (0) | 2020.04.09 |




