| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- binary search
- String
- two pointer
- Dijkstra
- DP
- union find
- Two Points
- Brute Force
- 이진탐색
- MYSQL
- 다익스트라
- Stored Procedure
- Trie
- 스토어드 프로시저
- SQL
- Hash
- 그래프
- Today
- Total
codingfarm
1. 소개 본문
패턴 인식의 가장 간단한 관점
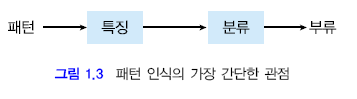
특징,분류 : 패턴인식에서 제일 중요한 2개의 주제
예 : 사람의 얼굴을 인식하기
얼굴이 작고, 코가 뾰족하고, 눈썹이 짙고, 눈이 작은 샘플이 있다면
- 특징
- 얼굴 크기($x_1$), 코의 모양($x_2$), 눈썹의 짙은 정도($x_3$), 눈의 크기($x_4$)
- 분류
- $x_1$ = 작다, $x_2$ = 뾰족하다, $x_3$ = 짙다, $x_4$ = 작다 라는 패턴이 들어왔을때, 이미 알고 있는 지식에 비추어 아무개일 가능성이 높다라는 의사 결정과정.
- M : 부류의 갯수
- $w_i$ : 각 부류
DB 수집
패턴 인식 시스템을 만들기 위해서는 pattern을 수집해야한다.
sample : 인식 시스템을 만들기 위해 수집한 패턴
DB에는 아래와 같은 2개의 집합이 있다.
- training set : 인식기를 만들기 위해 사용할 집합
- test set : 인식기를 평가하기 위해 사용하는 집합
DB가 양적/질적으로 우수해야 좋은 인식기를 만들 수 있다.
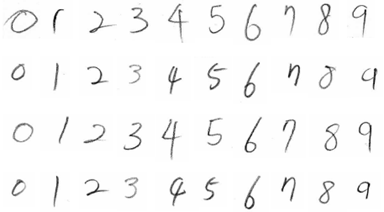

특징(feature)
샘플을 분류하기 위해서 패턴으로부터 추출해야할 특이사항

위의 8*8 비트맵에서 특징을 검출할 방법은 2가지가 있다.
1)각 비트별로 삼을경우 : $x = \left[x_1, x_2, ... , x_{64} \right]$
2)구역을 나눠서 0과 1의 비례로 파악 : $x = \left[x_1, x_2\right]$
$X$ : 특징 벡터(feature vector)
d : 특징의 갯수
[그림 1.5]는 2번째 방법으로 특징을 추출한것이다.
그렇게 얻은 특징으로 그래프상에 분류하면 아래와 같다.
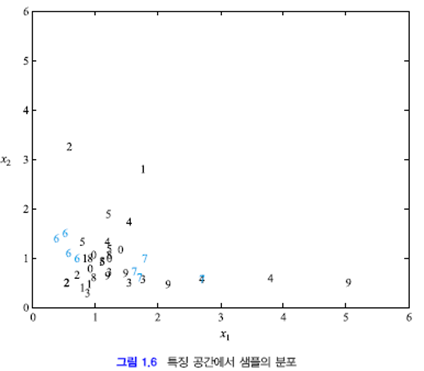
최고의 성능을 가진다고 하긴 힘들지만 6과 7은 잘 구분하는 것을 확인가능하다.
위와 같은 분포도를 통해 쓸모없는 특징과 각 특징의 중요도를 알 수 있다.
| 특징을 많이쓰면 | 적게 쓰면 |
| 분별력$\blacktriangle$, 계산량$\blacktriangledown$ | 분별력$\blacktriangledown$, 계산량$\blacktriangle$ |
특징을 분별함에 있어서 중요한 문제
- 분별력(discriminating power)
- 차원의 저주(curse of dimensinality)
특징을 얼마나, 어떻게 쓸것인지는 매우 중요하다.
8장과 9장에서 특징 추출 및 가공에 대해 배운다.
분류(classification)
어떤 패턴이 들어왔을때 특징을 통해서 M개의 부류중 하나로 할당하는 작업
분류기(classifier) : 분류를 담당하는 프로그램
특징공간이 2차원($x_1$, $x_2$)이며 부류도 2개($w_1$, $w_2$)가 있는 상황에서 $w_1$과 $w_2$는 각각 10개와 12개의 훈련 샘플을 가지고 있는 상황을 예로 들겠다. 이 분류 문제에서 두 부류를 어떻게 분류할 것인가?
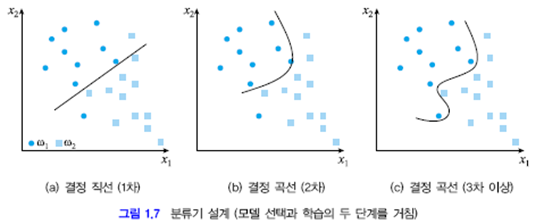
분류기 설계 과정
- 모델 선택(model selection)
- 분류기를 표현하는 수학적 모델로 무엇을 쓸지 결정한다.
- 위 그림은 1차~3차 이상의 결정직선 or 곡선을 쓰는것을 볼 수 있다.
- 성능 평가를 통해 적절한 분류기를 사용해야한다
- 다항 식 이외에 결정 경계를 만둘어주는 신경망이나 SVM 같은 분류 방법론이 있다.
- 분류기 학습(learning) or 훈련(training)
결정 직선(2차원), 결정 평면(3차원), 결정 초평면(4차원 이상)
- 경계식을 1차식으로 표현 가능한것
- 2개의 부류를 나누는데 주로 사용될 수 있다.
- 결정 초평면을 쓰는 분류기를 선형분류기(linear classifier) 라 한다.
비선형 분류기 : 2차 이상의 다항식으로 표현되는 분류기
-패턴인식은 학습용 샘플이 아닌 테스트용 샘플에서의 성능이 진정 가치있다.
-검증 집합(validation set) : 분류기 모델의 성능을 검증하는데 쓰인다.
-처음본 샘플에 대해 보여주는 성능을 일반화(generalization) 능력이라 한다.
위 그래프에서 제일 아래의 $w_1$ 샘플이 1,2차 경계선에선 $w_2$로 분류되지만 3차 경계선에선 $w_1$로 분류된다.
3차가 더 우수할 수 있지만 제일 아래쪽의 신호가 noise에 의한 외톨이일 가능성이 있으며 3차 결정 곡선은
과적합(over fitting) 되었다고도 볼 수 있다.
너무 복잡한 모델을 사용하여 훈련 집합에 과적합 시키는 일은 피하는것이 좋다(Occam의 칼날)
지도학습과 비지도학습
- 지도학습(supervised learning)
- 훈련 집합의 샘플이 자신이 속한 부류를 알 경우
- 분류기가 최소의 오류를 갖도록 weight와 bias를 조절하는게 목적
- 참부류(true class) : 검증 과정에 따라 사람이 부여하는 부류정보
- 비지도학습(unsupervised learning)
- 샘플의 부류 정보가 없다
- 비슷한 샘플을 집단으로 모으는것이 목적이다(군집화 : clustering)
성능 평가
패턴 인식 시스템의 성능은 크게 2가지 기준으로 측정한다.
1.맞추는 샘플, 틀리는 샘플, 기각하는 샘플의 수를 세서 그것을 이용한다.
$\displaystyle 정인식률(correct\;recognition\;rate) = \frac{c}{N} \\\displaystyle 기각률(rejection\;rate) = \frac{r}{N} \\ 오류율(error\;rate) = \frac{e}{N} \\\displaystyle 이때, c= 맞춘\;샘플\;수, r = 기각한\;샘플\;수, e = 틀린\;샘플\;수\\N=c+r+e$
오류경향을 더욱 세밀하게 분석하기 위해 혼동행렬(confusion matrix)를 사용한다.
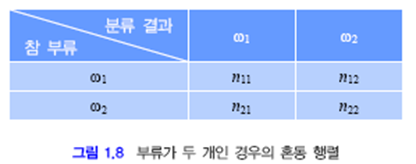
$n_{ij} : 부류 w_i에\;속하는\;샘플을\;w_j로\;분류한\;것의\;개수이다.$
$n_{ij}$에서
$i = j$ 이면 옳게 분류한 것
$i \neq j$ 이면 틀리게 분류한 것
이다
2.틀리게 분류하였을 때 발생하는 위험을 고려하여 위험(risk) 정도를 수치화한다.
-위험(risk)은 그 결과 손실(loss)을 발생 시키므로 이 둘은 같게 취급 할 수 있다.
-$n_{12}$와 $n_{21}$를 잘못 분류하는 경우, 우류률에 의하면 같게 취급하지만 이 둘은 질적으로 완전히 다르다.
(ex : 암환자를 정상으로 분류하는게 정상인을 암환자로 분류하는것 보다 위험도가 훨씬 더 크다.)
검출(detection)
특정패턴을 위해 분류기를 사용하는 목적이다.
$\left\{\begin{array}{}
w_1 : 찾고자\;하는\;샘플\\
w_2 : 그렇지\;않은\;샘플\\
\end{array}
\right.$
-결과
$\left\{\begin{array}{}
TP\;1) 참긍정(true\;positive) : w_1을 w_1으로\;옳게\;분석한\;샘플\\
TN\;2) 참부정(true\;negative) : w_2를 w_2로\;옳게\;분석한\;샘플\\
FN\;3) 거짓부정(false\;negative) : w_1을 w_2로\;틀리게\;분석한\;샘플\\
FP\;4) 거짓긍정(false\;positive) : w_2을 w_1으로\;틀리게\;분석한\;샘플\\
\end{array}
\right.$
거짓긍정은 거짓 검출(false detection; FD) 혹은 거짓 경보(false alarm; FA)라고도 한다.
-검출 시스템의 성능기준
거짓 긍정률 (false positive rate; FPR) = $\frac{n_{21}}{n_{21}+n_{22}}$
거짓 부정률 (false negative rate; FNR) = $\frac{n_{22}}{n_{12}+n_{11}}$
-검색 시스템의 성능기준
정확률(precision) = $\frac{n_{11}}{n_{11}+n_{21}}$
재현률(recall) = $\frac{n_{11}}{n_{11}+n_{22}}$

'AI > 패턴인식' 카테고리의 다른 글
| 3. 확률 분포 추정 - 파젠창(Parzen Window) (0) | 2020.04.10 |
|---|---|
| 3. 확률 분포 추정 - 히스토그램 추정(histogram estimation) (0) | 2020.04.10 |
| 3. 확률 분포 추정 - 최대 우도 추정(Maximum Likelihood Estimation) (0) | 2020.04.10 |
| 3. 확률 분포 추정-개요 (0) | 2020.04.09 |
| 2. 베이시언 결정 이론 (0) | 2020.01.29 |




