| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- String
- Hash
- union find
- 그래프
- 다익스트라
- Two Points
- Brute Force
- Stored Procedure
- Trie
- 이진탐색
- SQL
- two pointer
- MYSQL
- binary search
- Dijkstra
- 스토어드 프로시저
- DP
Archives
- Today
- Total
codingfarm
3. 확률 분포 추정 - 최근접 이웃 추정(k-nearest neighbours estimation) 본문
$\circ$ 파젠창은 고정된 크기의 창의 중심 $\mathscr x$를 어디에 두느냐에 따라 창안의 샘플수가 달라진다.
$\circ$ k-최근접 이웃법은 $\mathscr x$를 중심으로 샘플이 k개 들어올때 까지 창의 크기를 확장해나간다. $k$개가 들어온순간 창의 크기를 $h$라 한다.
| 파젠창 | k-최근접 이웃추정 |
| $h$고정, $k$가 $\mathscr x$에 따라 변화 | $k$ 고정, $h$가 $\mathscr x$에 따라 변화 |
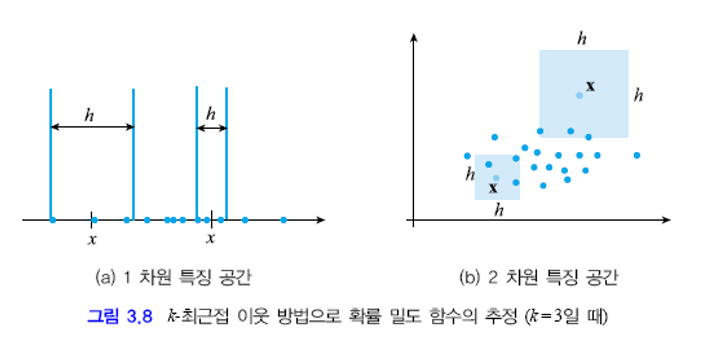
큰 $h$값을 가지는 $\mathscr x$ 주위에는 샘플이 희소하게 분포함을 뜻하므로 확률이 낮아야 하고
작은 $h$값을 가지는 $\mathscr x$ 주위에는 샘플이 빽빽하게 분포함을 뜻하므로 확률이 높아진다.
이 원리를 바탕으로 아래식을 활용하여 확률 분포의 추정이 가능하다.
$$p(\mathscr x)=\frac{1}{h_{\mathscr x}^d}\frac{k}{N}$$
$k$와 $N$은 $\mathscr x$에 무관하고 $h$가 $\mathscr x$에 따라 변하므로 $h_{\mathscr x}$로 표기한다.
이 방법을 위해 주어진 $\mathscr x$에 가장 가까운 $k$개의 샘플을 찾아야 한다.
시간 복잡도(time complexity)는 $\Theta(kdN)$이다.
즉, 훈련 집합의 크기가 크고 공간 차원이 높을때 계산량이 많다.
계산속도를 빠르게 하기 위해 훈련집합에 따라 특징공간을 미리 여러구간으로 나누어 놓는 보르노이 도형(vornoi diagram) 방법을 활용 할 수 있다.
'AI > 패턴인식' 카테고리의 다른 글
| 3. 확률 분포 추정 - 혼합 모델(mixture model) (3) | 2020.04.11 |
|---|---|
| 3. 확률 분포 추정 - 최근접 이웃 분류기(k-nearest neighbour(k-NN) classifier) (0) | 2020.04.11 |
| 3. 확률 분포 추정 - 파젠창(Parzen Window) (0) | 2020.04.10 |
| 3. 확률 분포 추정 - 히스토그램 추정(histogram estimation) (0) | 2020.04.10 |
| 3. 확률 분포 추정 - 최대 우도 추정(Maximum Likelihood Estimation) (0) | 2020.04.10 |
Comments




