| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- String
- 다익스트라
- Two Points
- two pointer
- SQL
- MYSQL
- DP
- Dijkstra
- union find
- 이진탐색
- Stored Procedure
- 그래프
- Brute Force
- 스토어드 프로시저
- Hash
- Trie
- binary search
- Today
- Total
codingfarm
3. 확률 분포 추정 - 혼합 모델(mixture model) 본문
지금까지 훈련집합 $X$로부터 확률분포를 추정하는 여러가지 방법을 공부하였다.
이 절에서는 앞에서 공부한 방법에 비해 색다르게 확률 분포 추정 방법을 다룬다.
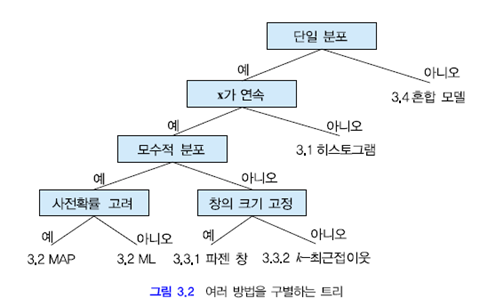
그림에서 보이듯이 혼합모델에서는 두개 이상의 서로 다른 확률 분포의 혼합으로 $X$를 모델링 한다.
가우시언 혼합(Gaussian Mixture)
가우시언이 여러개 혼합된 형태로 샘플이 주어질때 확률분포를 추정하는 방법이다.
주어진 값 $X=\{\mathscr x_1, \mathscr x_2 \cdots \mathscr x_N\}$
추정할 값 $\Theta=\{\pi=(\pi_1,\cdots,\pi_K),(\mu_1,\Sigma_1),\cdots,(\mu_k,\Sigma_k)\}$
즉, 샘플입력 $X$가 주어지면 몇개($k$)의 가우시언으로 샘플입력의 분포를 표현 가능할지 알아내야 하며 각각의 가우시언에 대한 요소분포와 혼합계수를 알아내야한다.
샘플집합 $X$에 대해 $K$개의 가우시언을 가진다면
$\displaystyle p(\mathscr x)=\sum_{k=1}^{K} \pi_k N(\mathscr x| \mu_k,\Sigma_k)$
$\mathscr x$는 샘플집합 $X$에 속하는 임의의 샘플이다.
요소 분포(Component Distribution)
$N(X|\mu_k,\Sigma_k)$
$\bullet$ $N(\mu_k,\Sigma_k)$가 $X$의 함수임을 명시하기 위한 표기법
$\bullet$ $k$번째 가우시안을 지칭
혼합계수(mixing coefficient)
$\pi_k$
$\bullet$ 총 샘플의 수($N$)와 $k$번째 가우시안에 속하는 샘플수($a_k$) 사이의 비
$\pi_k=\dfrac{a_k}{N}$
최대우도추정문제로 발전시키면 $X$를 발생시킬 가능성이 제일 큰 매개변수집합 $\Theta$를 찾아 그것을 $\hat \Theta$로 취하면 분류가 가능하다.
$\displaystyle \hat \Theta=\underset{\Theta}{argmax}\;\ln p(X|\Theta)$
$\displaystyle \ln p(X|\Theta)=\sum_{i=1}^{N}\ln\left( \sum_{k=1}^{K}\pi_kN(\mathscr x_i|\mu_k,\Sigma_k) \right)$

그림 3.10 (a)의 경우 하나의 가우시언 분포로 표현이 가능하다.
하지만 (b),(c)는 그렇지 못하다. 두개이상의 모드를 가진 분포를 최소의 오류로 모델링 하기 위해선 여러개의 가우시언 분포를 사용하는 방법이 있으며 이를 가우시언 혼합(Gaussian mixture)이라 한다.
발상은 간단하지만 수학적인 지식은 그렇지 못하다. 이제 실현 작업을 보겠다.

위 그림은 24개의 샘플의 분포를 나타내었다.
즉, 샘플의 집합 $X=\{\mathscr x_1,\mathscr x_2, \cdots,\mathscr x_N \}$ 이 있으며 $N=24$이다.
주어진 $X$를 가지고 추정해야 하는 매개 변수들은 아래와 같다.
가우 시언의 개수 $K$
$k$ 번째 가우시언의 매개변수 $(\mu_k, \Sigma_k),k=1,\cdots,K$
$k$ 번째 가우시언의 가중치 $\pi_k,k=1,\cdots,K$
세가지 매개변수들에 대해 차례로 살펴보자.
몇개의 가우시안을 쓸지는 자동으로 결정할 수도 있지만 여기서는 미리 고정되어 있다고 가정한다.
1. 그림 3.11 (c) 는 $K=2$인 경우를 보여주고 있다.
2. $K$개 각각의 평균 벡터 $\mu_k$와 공분산행렬 $\Sigma_k$를 구한다.
3. 가우시언 각각의 영향력을 나타내는 가중치이다. 그림 3.1(c)를 보면 아랫쪽에 있는 가우시언 $N(\mu_1,\Sigma_1)$과 윗 쪽의 가우시언 $N(\mu_2,\Sigma_2)$에서 생성된걸로 보이는 샘플은 각각 8개와 16개다. 따라서 윗쪽 가우시언에서 발생할 확률이 아랫쪽의 것보다 2배 정도 크다고 할 수 있다. 그러므로 첫번째와 두번째 가우시언의 가중치를 각각 $1/3$과 $2/3$으로 볼 수 있다.
3개의 매개변수를 바탕으로 $X$의 확률을 구하면 아래와 같다.
$\displaystyle p(\mathscr x)=\frac{1}{3}N(\mu_1,\Sigma_1)+\frac{2}{3}N(\mu_2,\Sigma_2)$
위 수식을 일반적인 경우로 확장하면
$\displaystyle p(\mathscr x)=\sum_{k=1}^{K} \pi_k N(\mathscr x| \mu_k,\Sigma_k)$
$N(\mu_k,\Sigma_k)$가 $\mathscr x$의 함수임을 명시하기 위해 $N(\mathscr x| \mu_k,\Sigma_k)$로 표기하였다.
$N(\mathscr x| \mu_k,\Sigma_k)$를 기본요소로 하여 혼합 분포가 만들어 지므로 각각의 가우시언을 요소 분포(component distribution)라 부른다. 요소 분포는 가우시언 분포뿐만 아니라 베르누이 분포 등 어떠한 분포라도 사용 가능하나 여기선 가우시언으로 국한하여 설명한다. 실제로 가우시언을 제일 많이 사용한다.
$\pi_k$는 가중치로서 혼합계수(mixing coefficient)라 부른다. 혼합계수 또한 확률 값 이므로 $0 \leq \pi_k \leq 1$과 $\displaystyle \sum_{k=1}^{K}\pi_k=1$ 의 두가지 조건을 만족해야 한다.
이제 주어진 값과 추정해야 할 값을 다시 정리하여 문제를 명확히 해보자.
주어진 값 $X=\{\mathscr x_1, \mathscr x_2 \cdots \mathscr x_N\}$
추정할 값 $\Theta=\{\pi=(\pi_1,\cdots,\pi_K),(\mu_1,\Sigma_1),\cdots,(\mu_k,\Sigma_k)\}$
즉, 샘플입력 $X$가 주어지면
몇개($k$)의 가우시언으로 샘플입력의 분포를 표현 가능할지 알아내야 하며
각각의 가우시언에 대한 요소분포와 혼합계수를 알아내야한다.
이제 최적화 문제를 정의하는데 필요한 재료를 모두 확보하였다.
이들을 이용하여 최대 우도(ML) 추정 문제로 발전시켜보자.
각 샘플집합이 독립적일경우
$\displaystyle \begin{align*}
P(X|\Theta) =P(\mathscr x_1, \mathscr x_2,\cdots, \mathscr x_N|\Theta) &=P(\mathscr x_1|\Theta) P(\mathscr x_2|\Theta)\cdots P(\mathscr x_N|\Theta) \\
&=\prod_{i=1}^{N} P(\mathscr x_i | \Theta)
\end{align*}$
그리고
$\displaystyle P(\mathscr x| \Theta) = P(\mathscr x|\Theta_1) + P(\mathscr x|\Theta_2) + \cdots + P(\mathscr x|\Theta_K) = \sum_{k=1}^{K} P(\mathscr x | \Theta_k)$
그러므로 매개변수 집합 $\Theta$에 대한 $X$의 우도를 아래와 같이 쓸 수 있다.
$\displaystyle p(X|\Theta)=\prod_{i=1}^{N}p(\mathscr x_i|\Theta)=\prod_{i=1}^{N}\left( \sum_{k=1}^{K}\pi_kN(\mathscr x_i|\mu_k,\Sigma_k) \right)$
곱 연산을 합연산으로 바꾸기 위해 로그 우도 형태로 다시쓰면
$\displaystyle \ln p(X|\Theta)=\sum_{i=1}^{N}\ln\left( \sum_{k=1}^{K}\pi_kN(\mathscr x_i|\mu_k,\Sigma_k) \right)$
이제 문제를 '$X$에 대해 최대 우도를 갖는 $\Theta$를 찾는'것으로 정의할 수 있게 되었다. 말로 다시 풀어 보면 관찰된 $X$가 있는데 이것을 발생시켰을 가능성이 가장 큰 매개변수 집합 $\Theta$를 찾아 그것을 $\hat \Theta$로 취하라는 의미이다.
$\displaystyle \hat \Theta=\underset{\Theta}{argmax}\;\ln p(X|\Theta)$
지금까지 최적화 문제를 유도하였고 그와 관련된 모든 수식을 제시하였다.
다음포스팅에서 최적화 문제를 풀기위한 EM 알고리즘에 대해 다루겠다.
'AI > 패턴인식' 카테고리의 다른 글
| 3. 확률 분포 추정 - 최근접 이웃 분류기(k-nearest neighbour(k-NN) classifier) (0) | 2020.04.11 |
|---|---|
| 3. 확률 분포 추정 - 최근접 이웃 추정(k-nearest neighbours estimation) (0) | 2020.04.11 |
| 3. 확률 분포 추정 - 파젠창(Parzen Window) (0) | 2020.04.10 |
| 3. 확률 분포 추정 - 히스토그램 추정(histogram estimation) (0) | 2020.04.10 |
| 3. 확률 분포 추정 - 최대 우도 추정(Maximum Likelihood Estimation) (0) | 2020.04.10 |




