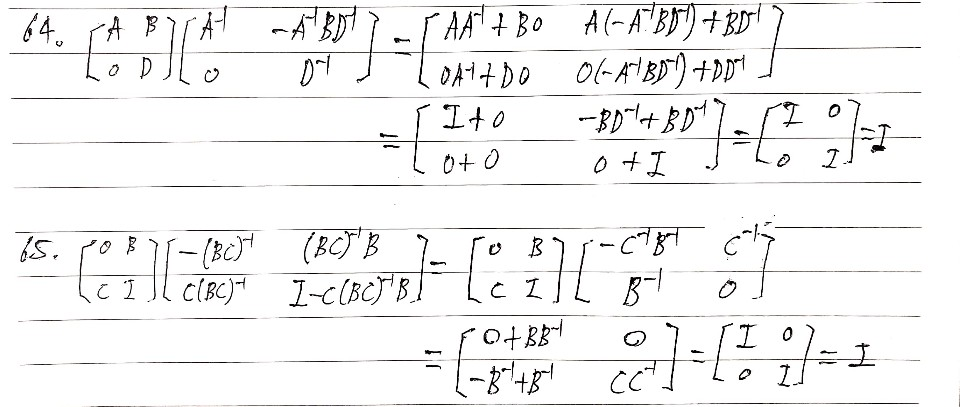| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- Hash
- MYSQL
- two pointer
- 이진탐색
- binary search
- DP
- SQL
- 다익스트라
- Two Points
- String
- Stored Procedure
- Brute Force
- Trie
- union find
- 스토어드 프로시저
- 그래프
- Dijkstra
- Today
- Total
codingfarm
역행렬(Inverse Matrix) 본문
$A$가 $n \times n$ 행렬일때, $A$의 역행렬은
$AA'=I, A'A=I$
를 만족하는 $n \times n$행렬 $A'$ $I=I_n$은 $n \times n$ 단위행렬이다.
$A$의 역행렬 $A'$가 존재하면, $A$를 가역(invertible)이라고 한다.
| $A$가 가역행렬이면 $A$의 역행렬은 유일하다. |
증명
$A$가 서로 다른 두개의 역행렬 $A'$과 $A''$를 갖는다 가정한다.
$AA'=I=A'A, AA''=I=A''A$
$A'=A'I=A'(AA'')=(A'A)A''=IA''=A''$
$A'=A''$ 이므로 두행렬이 서로 다르다는 가정에 위배된다.
그러므로 $A$의 역행렬이 존재하면 유일하다. $\blacksquare$
경고
$A^{-1}$은 $\displaystyle \frac{1}{A}$로 나타내지 않는다. 역함수와 역수는 분명 다른 개념이다.
| $A$가 $n \times n$가 역행렬이면 $Ax=b$로 주어진 연립일차방정식은 $\mathbb R^n$의 임의의 $b$에 대하여 유일한 해 $x=A^{-1}b$를 갖는다. |
|
$\displaystyle A=\begin{bmatrix}a & b \\c & d \end{bmatrix}$ 일 때, $A$가 가역일 필요충분 조건은 $ad-bc \neq 0$ 이고, 이 경우에 $A$의 역행렬은 $\displaystyle A^{-1}=\frac{1}{ad-bc} \begin{bmatrix}d &-b \\ -c& a \end{bmatrix}$ $ad-bc$는 A의 행렬식(determinant)라고 한다. |
가역행렬의 성질
|
a. $A$가 가역행렬이면 $A^{-1}$도 가역행렬이다 $$(A^{-1})^{-1}=A$$ b. $A$가 가역행렬이고 $c$가 0이 아닌 스칼라이면, $cA$도 가역행렬이다 $$\displaystyle (cA)^{-1}=\frac{1}{c}A^{-1}$$ c.$A$와 $B$가 같은 크기의 가역행렬이면, $AB$도 가역행렬이다 $$(AB)^{-1}=B^{-1}A^{-1}$$ d. $A$가 가역행렬이면 $A^T$도 가역행렬이다 $$(A^T)^{-1}=(A^{-1})^T$$ e. $A$가 가역행렬이면, 음이 아닌 모든 정수 $n$에 대하여 $A^n$도 가역행렬이다 $$(A^n)^{-1}=(A^{-1})^n$$ |
$A$가 가역행렬이고 $n$이 양의 정수이면 $A^{-n}$은
$$A^{-n}=(A^{-1})^n=(A^n)^{-1}$$
로 정의한다.
기본행렬(elementary matrix)
기본행렬은 단위행령에 한번의 기본 행 변환을 적용하여 얻을수 있느 ㄴ행렬이다.
기본 행 변환은 세가지가 있다. 곱하기, 바꾸기, 사칙연산
$\displaystyle E_1= \begin{bmatrix}
1&0&0&0\\
0&3&0&0\\
0&0&1&0\\
0&0&0&1
\end{bmatrix}$ 은 $I$를 $3R_2$ 한것이다.
$\displaystyle E_2= \begin{bmatrix}
0&0&1&0\\
0&1&0&0\\
1&0&0&0\\
0&0&0&1
\end{bmatrix}$ 은 $I$를 $R_1 \leftrightarrow R_3$ 한것이다.
$\displaystyle E_3=\begin{bmatrix}
1&0&0&0\\
0&1&0&0\\
0&0&1&0\\
0&-2&0&1
\end{bmatrix}$ 은 $I$를 $R_4-2R_2$한것이다.
임의의 행렬 A가 주어질때 A에 기본행렬을 곱함으로써 기본행변환을 얻은 효과를 얻을 수 있다.
$\displaystyle A = \begin{bmatrix}
a_{11}&a_{12}&a_{13}&a_{14}\\
a_{21}&a_{22}&a_{23}&a_{24}\\
a_{31}&a_{32}&a_{33}&a_{34}\\
a_{41}&a_{42}&a_{43}&a_{44}
\end{bmatrix}$
$\displaystyle E_1A = \begin{bmatrix}
a_{11}&a_{12}&a_{13}&a_{14}\\
3a_{21}&3a_{22}&3a_{23}&3a_{24}\\
a_{31}&a_{32}&a_{33}&a_{34}\\
a_{41}&a_{42}&a_{43}&a_{44}
\end{bmatrix}$
$\displaystyle E_2A = \begin{bmatrix}
a_{31}&a_{32}&a_{33}&a_{34}\\
a_{21}&a_{22}&a_{23}&a_{24}\\
a_{11}&a_{12}&a_{13}&a_{14}\\
a_{41}&a_{42}&a_{43}&a_{44}
\end{bmatrix}$
$\displaystyle E_3A = \begin{bmatrix}
a_{11}&a_{12}&a_{13}&a_{14}\\
a_{21}&a_{22}&a_{23}&a_{24}\\
a_{31}&a_{32}&a_{33}&a_{34}\\
a_{41}-2a_{21}&a_{42}-2a_{22}&a_{43}-2a_{23}&a_{44}-2a_{24}
\end{bmatrix}$
| $E$가 $I_n$에 한번의 기본행변환을 해서 얻은 기본행렬일 경우, 같은 기본행변환을 $n \times n$행렬 $A$에 적용하면, 그 결과는 행렬 $EA$와 같다. |
가역행렬의 기본정리
|
$A$가 $n \times n$행렬일때 다음 명제들은 동치이다. (즉, 하나라도 참이면 나머지도 다 참이다.) a. $A$는 가역행렬이다. b. $\mathbb R^n$의 임의의 $b$에 대하여, $AX=b$는 유일한 해를 갖는다. c. $AX=0$의 해는 자명해 뿐이다.(해가 0 뿐이다.) d. $A$의 기약행사다리꼴은 $I_n$이다. e. $A$는 기본행렬들의 곱이다. |
| $A$가 정사각행렬이라 하자, $B$가 $AB=I$ 또는 $BA=I$인 정사각행렬이라 하면, $A$는 가역행렬이고 $B=A^{-1}$이다. |
| $A$가 정사각행렬이라 하자, 일련의 기본행변환이 $A$를 단위행렬 $I$로 변형시키면 일련의 동일한 기본행변환은 $I$를 $A^{-1}$로 바꾼다. |
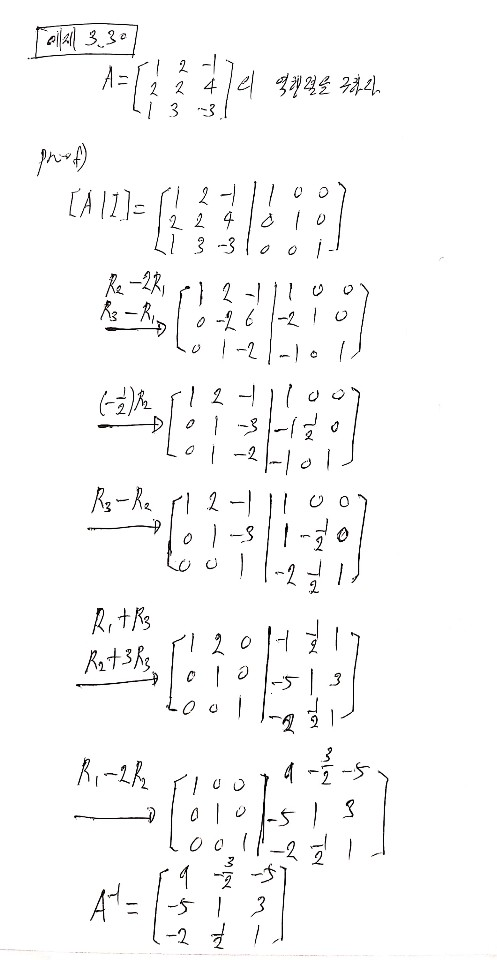
가우스-조르당 소거법을 이용한 역행렬 구하기
$A$와 $I$로 첨가행렬 $[A|I]$를 만들어 동시에 행변환 한다.
$[A|I] \rightarrow [I|A^{-1}]$
$A$가 $I$로 변할수 없으면 $A$는 비가역적이다.
'수학 > 선형대수학' 카테고리의 다른 글
| 부분공간 (0) | 2020.05.07 |
|---|---|
| LU 분해(LU factorization) (2) | 2020.04.15 |
| 행렬 대수 (0) | 2020.04.01 |
| 연립 일차 방정식 (0) | 2020.03.06 |
| 벡터 - 직선과 평면 (0) | 2020.03.01 |