| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- Hash
- 다익스트라
- binary search
- union find
- Dijkstra
- 스토어드 프로시저
- Trie
- String
- Stored Procedure
- MYSQL
- Two Points
- DP
- two pointer
- SQL
- Brute Force
- 그래프
- 이진탐색
- Today
- Total
codingfarm
4.3 조건부 분포(Conditional Distribution) 본문
$X$와 $Y$가 공간 $S$에서 $joint\;pmf\;f(x,y)$를 가진다.
marginal pmf는 공간 $S_X$와 $S_Y$에서 각각 $f_X(x),\;f_Y(y)$이다.
사건(event)$A = \{X=x\},\;B=\{Y=y\},\;(x,y) \in S$일때
$A \cap B = \{X=x, Y=y\}$ 이다.
왜냐하면
$$P(A \cap B) = P(X=x,\;Y=y)=f(x,y)$$
그리고
$$P(B)=P(Y=y) = f_Y(y)>0\;\;\;(since\;Y \in S_Y)$$
일 경우
사건 $B$가 주어질때 사건 $A$의 조건부확률(Conditional Probability)는
$$P(A|B)=\dfrac{P(A \cap B)}{P(B)}=\dfrac{f(x,y)}{f_Y(y)}$$
이다.
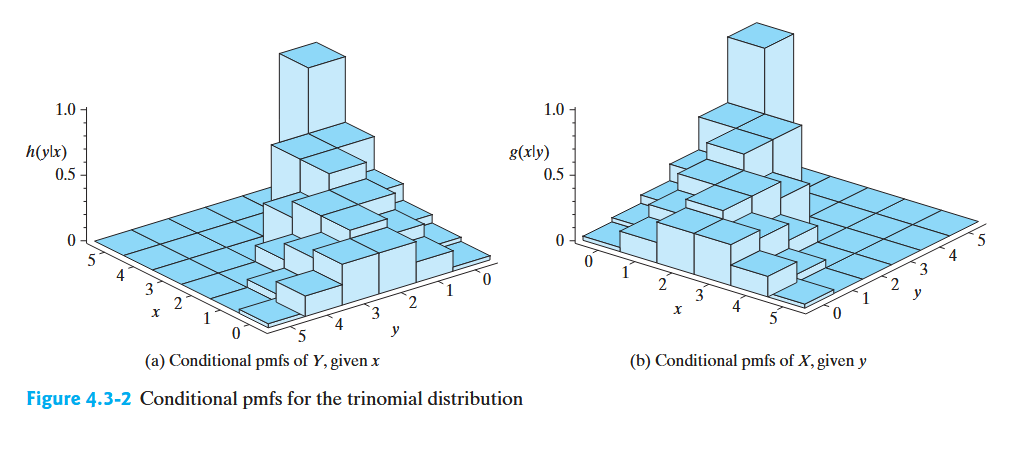
$Y=y$가 주어질때 $X$의 조건부 확률 질량 함수(Conditional pmf)는 아래처럼 정의된다.
$$g(x|y)=\dfrac{f(x,y)}{f_Y(y)},\;\;\;f_Y(y)>0$$
유사하게 $X=x$가 주어질 때 $Y$의 conditional pmf는 아래처럼 정의된다.
$$h(y|x)=\dfrac{f(x,y)}{f_X(x)},\;\;\;f_X(x)>0$$
conditional pmf도 확률이므로 확률의 법칙을 따른다
$$0 \leq h(y|x) \leq 1 \\ \sum_y h(y|x) = \sum_y \dfrac{f(x,y)}{f_X(x)}=\dfrac{f_X(x)}{f_X(x)}=1$$
$P(a< Y < b | X=x) = \sum_(y:a<y<b)h(y|x)$
조건부 기댓값(conditional expectation)의 경우
$E[Y|X=x] = \sum_y y \; h(y|x)$
그러므로
$E[u(Y)|X=x]=\sum_yu(y)h(y|x)$
$X=x$가 주어젔을때 $Y$의 conditional expectation value 들은 아래와 같다,
$\mu_{Y|x}=E(Y|x)=\sum_yy\;h(y|x)$
$\begin{align*}
\sigma_{Y|X}^2&=E\{[Y-E(Y|x)]^2|x\}=\sum_y[y-E(Y|x)]^2h(y|x)
\\&=E(Y^2|x)-[E(Y|x)]^2
\end{align*}$
$E(Y^2|x)=\sum_y y^2 h(y|x)$
$E(Y|x)=\sum_y y \; h(y|x)$
$Y=y$일때 $X$의 conditional mean은 변수 $y$에 대한 함수이다.
$X=x$일때 $Y$의 conditional mean은 변수 $x$에 대한 함수이다.
후자의 경우는 함수가 $x$의 linear function이라고 가정한다.
즉, $E(Y|x) = a+bx$의 형태를 띈다
위식에서 나오는 $a$와 $b$를 $\mu_X,\;\mu_Y,\;\sigma_X^2\;,\sigma_Y^2,\;\rho$
의 항으로 표현해보자.
$\rho = \dfrac{E(XY)}{\sigma_X \sigma_Y}$
위식에서 표준편차(standard deviation) $\sigma_X$와 $\sigma_Y$는 둘다 양수다.
추정하면 분모가 0이 아니므로 상관계수(correlation coefficient)는 존재한다.
$\mu_{Y|x}=E(Y|x)=\sum_y y\; h(y|x) = \sum y \; \dfrac{f(x,y)}{f_X(x)}=a + bx, \;\;\;\;for\;x \in S_x$
$S_X$는 $X$의 공간이고 $S_Y$는 $Y$의 공간이다. 그 결과
$\mu_{Y|x}f_X(x)=\sum_y y\;f(x,y)=(a+bx)f_X(x),\;\;\;for \; x \in S_X\;\; \cdots \cdots(1)$
그리고
$$\begin{align*}
\mu_{{}_Y} = \sum_{x \in S_X} \sum_y y\;f(x,y)= \sum_{x \in S_X}(a+bx)f_X(x) &= \sum_{x \in S_X}af_X(x) + \sum_{x \in S_X}bx f_X(x) \\
&=a+b \mu_{{}_X}
\end{align*}$$
그러므로
$\mu_{{}_Y}= a + b \mu_{{}_X} \; \cdots \cdots (2)$
앞서 구한식 $\sum_y y\; f(x,y)=(a+bx)f_X(x)$를 통해
아래식을 구할 수 있다.(양변에 $x$의 합을 곱한다)
$\displaystyle \sum_{x \in S_X} \sum_y x y f(x,y) = \sum_{x \in S_X}(ax + bx^2)f_X(x)$
그러면
$E(XY) = aE(X) + bE(X^2)$
$\sigma_X^2 = E(X^2) - \{E(X)\}^2 = E(X^2) - \mu_{{}_X}^2$
이므로
$E(X^2) = \sigma_{{}_X}^2 + \mu_{{}_X}^2$
그리고
$\displaystyle \begin{align*}
\rho = \dfrac{Cov(X,Y)}{\sigma_{{}_X} \sigma_{{}_Y}} = \dfrac{E(XY)-E(X)E(Y)}{\sigma_{{}_X}\sigma_{{}_Y}} &= \dfrac{aE(X)+bE(X^2)-E(X)E(Y)}{\sigma_{{}_X}\sigma_{{}_Y}}
\\&=\dfrac{a \mu_{{}_X} + b(\sigma_{{}_X}^2 + \mu_{{}_X}^2) - \mu_{{}_X} \mu_{{}_Y}}{\sigma_{{}_X} \sigma_{{}_Y}}
\end{align*}$
$\displaystyle \mu_{{}_X} \mu_{{}_Y} + \rho \sigma_{{}_X} \sigma_{{}_Y} = a \mu_{{}_X} + b(\sigma_{{}_X}^2 + \mu_{{}_X}^2)\; \cdots \cdots \; (3)$
식 $(2)$와 $(3)$을 통해서
$a=\mu_{{}_Y}-\rho \dfrac{\sigma_{{}_Y}}{\sigma_{{}_Y}} \;\; and \;\; b=\rho \dfrac{\sigma_{{}_Y}}{\mu_{{}_X}}$
만약 $E(Y|x)$가 linear 하다면 아래식과 같음을 암시 가능하다.
$$E(Y|x) = \mu_{{}_Y} + \rho \dfrac{\sigma_{{}_Y}}{\sigma_{{}_X}}(x - \mu_{{}_X})$$
반대의 경우는
$$E(X|y) = \mu_{{}_X} + \rho \dfrac{\sigma_{{}_X}}{\sigma_{{}_Y}}(y - \mu_{{}_Y})$$
위 식에서 각 직선은
$x = \mu_{{}_X}$, $E(Y|x = \mu_{{}_X}) = \mu_{{}_Y}$을 지나고
$y = \mu_{{}_Y},\; E(X|y = \mu_{{}_Y}) = \mu_{{}_X}$을 지난다는 점에서
두 직선은 각각 $(\mu_{{}_X}, \mu_{{}_Y})$을 지남을 알 수 있다.
게다가 $E(Y|x)$에서 $x$의 계수인 $\displaystyle \rho \dfrac{\sigma_{{}_Y}}{\sigma_{{}_X}}$와
$E(X|y)$에서 $y$의 계수인 $\displaystyle \rho \dfrac{\sigma_{{}_X}}{\sigma_{{}_Y}}$ 의 곱은
$\rho^2$과 같음을 알 수 있다.
그리고 이들의 비율은 $\displaystyle \dfrac{\sigma_{{}_Y}^2}{\sigma_{{}_X}^2}$과 같다,
이 직관은 아래와 같은 예제에서 유용히 쓰인다.
'통계학 > 수리통계학' 카테고리의 다른 글
| 피어슨 상관 계수(Pearson Correlation Coefficient) (0) | 2020.08.14 |
|---|---|
| 이산형 이변량 분포(Bivariate Distribution of The Discrete Type) (0) | 2020.07.01 |
| 정규 분포(Normal Distribution) (0) | 2020.06.24 |
| 연속형 확률분포 - 카이제곱분포(chi-square distribution) (0) | 2020.04.30 |
| 연속형 확률분포 - 감마분포(The Gamma Distributions) (0) | 2020.04.23 |