| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- two pointer
- MYSQL
- 스토어드 프로시저
- Stored Procedure
- String
- 이진탐색
- binary search
- Brute Force
- Two Points
- DP
- SQL
- 그래프
- Trie
- Dijkstra
- Hash
- 다익스트라
- union find
- Today
- Total
codingfarm
1.단위 임펄스 및 단위 계단함수 본문
이산시간단위 임펄스 및 단위계단 순차열
단위 임펄스(unit impulse) : $\displaystyle \delta[n]=\begin{cases}0 & n \neq 0\\1 & n = 0\end{cases}$

단위 계단(unit step) : $\displaystyle u[n]=\begin{cases}0 &,n<0 \\1&, n \geq0 \end{cases}$

$\delta[n]=u[n]-u[n-1]$
$\displaystyle u[n]=\sum_{m=-\infty}^{n}\delta[m]=\sum_{k=\infty}^{0}\delta[n-k]=\sum_{k=0}^{\infty}\delta[n-k]$
수열의 합 구간 내에 $\delta[0]$이 포함되면 $u[n]$ 은 $1$이되고 그렇지 않으면 $0$이 된다.
$\sum_{m=-\infty}^{n} \delta[m]$ : impulse 신호는 고정되어있고 구간이 가변적이다. 그러므로 합이 $1$이 되기 위해선 $-\infty \sim n$에 $\delta[0]$이 들어와야 하므로 $n>0$ 이어야 한다.
$\sum_{k=0}^{\infty} \delta[n-k]$ : 구간은 정해저 있으며 impuse 신호의 위치가 가변적이다. 그러므로 합이 $1$이 되기 위해선 $0 \sim \infty$에 $\delta[0]$이 들어와야 하므로 $n=k$가 만족되어야 한다. 이를 위해 $n \geq 0$이어야 한다.
$\displaystyle \delta[n-k]=\begin{cases}0 &, n \neq k \\ 1 &, n=k \end{cases}$


단위 임펄스의 샘플링 성질
$\displaystyle x[n]\delta[n]=x[0]\delta[n]\\
x[n]\delta[n-n_0]=x[n_0]\delta[n-n_0]$
연속시간 단위계단 및 임펄스 함수
$\displaystyle u(t)=\begin{cases}0 &, t<0 \\1&, t\geq0 \end{cases}$

$\displaystyle u(t)=\int_{-\infty}^{t}\delta(\tau)d \tau = \int_{\infty}^{0}\delta(t-\sigma)d\sigma,\\ \displaystyle u(t)=\int_{0}^{\infty}\delta(t-\sigma)d\sigma$
적분 구간 내에 $\delta(0)$이 포함되면 $u(t)$는 $1$이 되고 그렇지 않으면 $0$이 된다.
$\int_{-\infty}^{t}\delta(\tau) d \tau$가 $1$이 되기 위해선 적분구간에 $\delta(0)$가 포함되어야 한다. 그러므로 $t \geq 0$ 이어야 적분값이 1이 될 수 있다.
$\int_0^\infty \delta(t - \sigma) d \sigma$가 1이 되기 위해선 적분구간에 $\delta(0)$가 포함되어야 한다. 즉, $t = \sigma$ 가 만족되야 하며 $\sigma$는 $0 \sim \infty$ 사이의 수이므로 $t$가 $0$ 이상이어야 적분값이 $1$이 될 수 있다.
$\displaystyle \delta(t)=\frac{du(t)}{dt}=\begin{cases}\infty &, t=0 \\0 &,t\neq0 \end{cases}$
연속시간 단위 임펄스 함수는 연속시간 계단 함수의 일차도함수와 같다.
$u(t)$는 불연속적이고 원칙적으로 미분이 불가능하다.
그러므로 $u(t)$는 근사적으로 이해해야 한다.

$\displaystyle \delta_\triangle=\frac{du_\triangle(t)}{dt}=\begin{cases}\frac{1}{\triangle} &,0<t<\triangle \\0&,otherwise \end{cases}$
$\delta(t)$는 $\delta_\triangle(t)$에서 $\triangle$가 매우 작을때의 펄스를 이상화 한것이라 볼 수 있다.
배율 변화된 임펄스 $k\delta(t)$는 면적이 $k$이고 아래식과 같이 나타낼 수 있다.
$\displaystyle \int_{-\infty}^{t}k\delta(\tau)d\tau=ku(t)$

앞에서 보았던 식
$\displaystyle u(t)=\int_{-\infty}^{t}\delta(\tau)d\tau$
는 그래프를 이용하여 도식적으로 해석이 가능하다.

$\sigma=t-\tau$로 바꿀경우
$\displaystyle u(t)=\int_{-\infty}^{t}\delta(\tau)d\tau=\int_{\infty}^{0}\delta(t-\sigma)(-d\sigma)\\
\displaystyle u(t)=\int_{0}^{\infty}\delta(t-\sigma)d\sigma$
$\delta(t-\sigma)$의 면적이 $\sigma=t$에 집중되어 있으므로
$t<0$에 대해서 0, $t>0$에 대해 1이다.
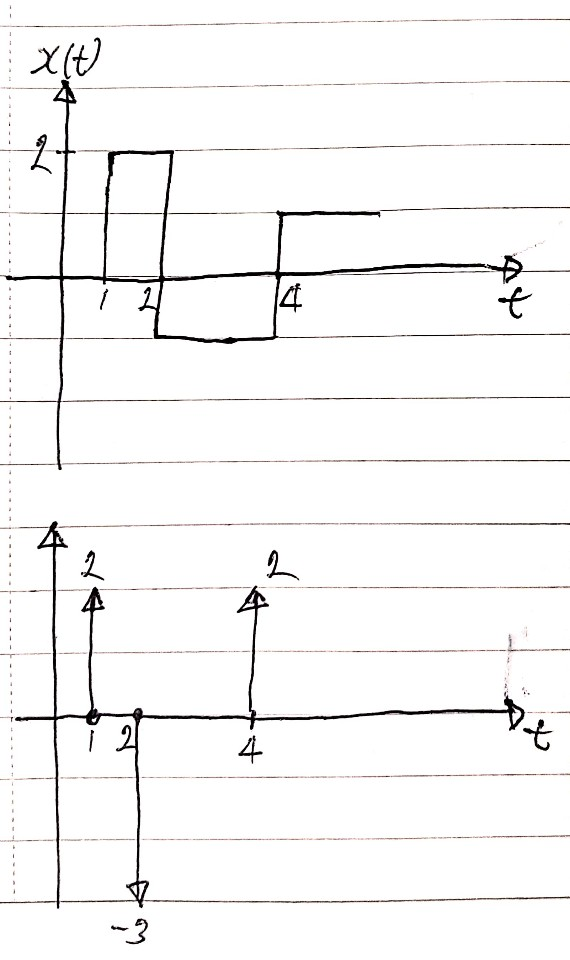
이산시간 임펄스의 샘플링 특성
$x_1(t)\delta_\triangle(t)=x(0)\delta_\triangle(t)$
- t의 구간이 $0\leq t \leq\triangle$가 아닌곳에서는 0이 된다
- $\triangle$이 충분히 작기에 $0\leq t \leq\triangle$ 구간내의 값은 일정하다
즉,
$x(t)\delta_\triangle(t) \approx x(0)\delta_\triangle(t)$
위 식에서 $\triangle \rightarrow 0$ 일때
$x(t)\delta_\triangle(t) = x(0)\delta_\triangle(t)$
을 만족한다
$t_0$에 집중된 임펄스에 대해선
$x(t)\delta(t-t_0) = x(t_0)\delta(t-t_0)$
즉, 임의의 신호 $x(t)$와 $x[n]$은 아래와 같이 표현 가능하다.
$$x(t)=\int_{-\infty}^{\infty}x(\tau)\delta(t-\tau)d\tau$$
$$x[n]=\sum_{k=-\infty}^{\infty}x[k]\delta[n-k]$$
'신호 및 시스템' 카테고리의 다른 글
| 2. 선형 시불변 시스템(LTI system) - 이산시간 LTI 시스템: 컨볼루션 합(Convolution Sum) (0) | 2020.04.18 |
|---|---|
| 2. 선형 시불변 시스템(LTI system) - 서론 (0) | 2020.04.18 |
| 1장. 연습문제 (0) | 2020.04.17 |
| 1. 연속시간 및 이산시간 시스템 (0) | 2020.03.28 |
| 1.신호와 시스템 (1) | 2020.03.25 |



