| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 스토어드 프로시저
- Dijkstra
- DP
- union find
- String
- SQL
- Trie
- Two Points
- Stored Procedure
- 다익스트라
- binary search
- 이진탐색
- 그래프
- two pointer
- MYSQL
- Brute Force
- Hash
- Today
- Total
codingfarm
1.신호와 시스템 본문
-우리는 연속시간 신호(continuous time signal; cts)와 이산시간 신호(discrete time signal; dts) 라는 기본적인 두가지 형태의 신호를 고려할것이다.
-cts의 경우 독립변수가 연속적이기 때문에 이 신호는 연속적인 독립변수 값으로 정의된다.
-dts의 경우 이산시간에서만 정의되고 독립변수는 오직 이산적인 값만을 갖는다.


| 연속 시간 신호 : $x(t)$ | 이산 시간 신호 : $x[n]$ |
| 독립변수(t)가 연속적이다 ($t \in \mathbb R$) | 독립변수(n)가 이산적이다.($n \in \mathbb Z$) |
신호 에너지와 파워
연속시간(continuous time)
- 연속시간 $t_1 \leq t \leq t_2$ 구간에 대한 총 에너지
$\displaystyle E=\int_{t_1}^{t_2}|x(t)|^2dt$
-무한구간 $-\infty < t < \infty$의 경우
$\displaystyle E_\infty=\lim_{T \rightarrow \infty} \int_{-T}^{T}|x(t)|^2dt=\int_{-\infty}^{\infty}|x(t)|^2dt$
-무한한 구간에 대한 시간 평균 파워
$\displaystyle P_\infty=\lim_{T \rightarrow \infty}\frac{1}{2T} \color{blue}{ \underbrace{\color{black} {\int_{-T}^{T}|x(t)|^2dt}}_{=E_\infty}}$
이산시간(discrete time)
-이산시간 $n_1 \leq n \leq n_2$ 구간에 대한 총에너지
$\displaystyle E=\sum_{n=n_1}^{n_2}|x[n]|^2$
-무한 구간 $-\infty < n < \infty$의 경우
$\displaystyle E_\infty=\lim_{N \rightarrow \infty} \sum_{n=-N}^{N}|x[n]|^2=\sum_{n=-\infty}^{\infty}|x[n]|^2$
-무한한 구간에 대한 시간 평균 파워
$\displaystyle P_\infty=\lim_{N \rightarrow \infty}\frac{1}{2N+1}\color{blue}{ \underbrace{\color{black}{ \sum_{n=-N}^{N}|x[n]|^2}}_{=E_\infty}}$
독립 변수의 변환
1)시간이동(time shift)
$\displaystyle x(t) \rightarrow x(t-t_0)$

$\displaystyle x[n] \rightarrow x[n-n_0]$

2)시간반전(time revarsal)
$\displaystyle x(t) \rightarrow x(-t), x[n] \rightarrow x[-n]$
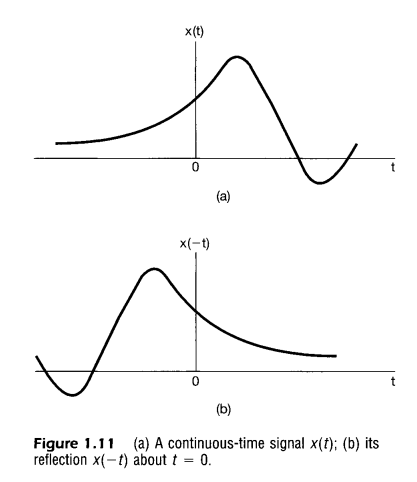
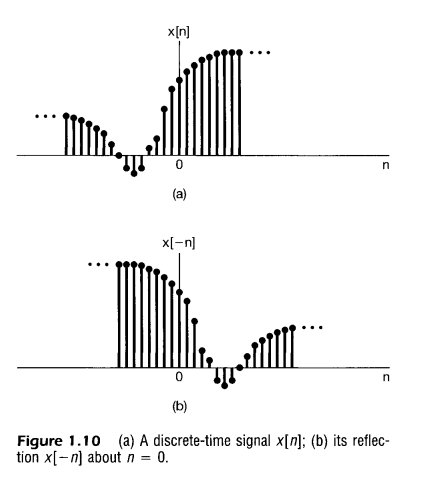
3) 시간 스케일링(time scaling)
$x(t) \rightarrow x(at), x[n] \rightarrow x[an]$

주기 신호(Periodic Signal)
특정 시간을 기준으로 값이 반복되는, T만큼 시간이동을 해도 값이 변하지 않는 신호이다.
$\displaystyle x(t) = x(t+T), x[n] = x[n+N]$
위 식을 만족하는 신호를 주기신호라 한다.
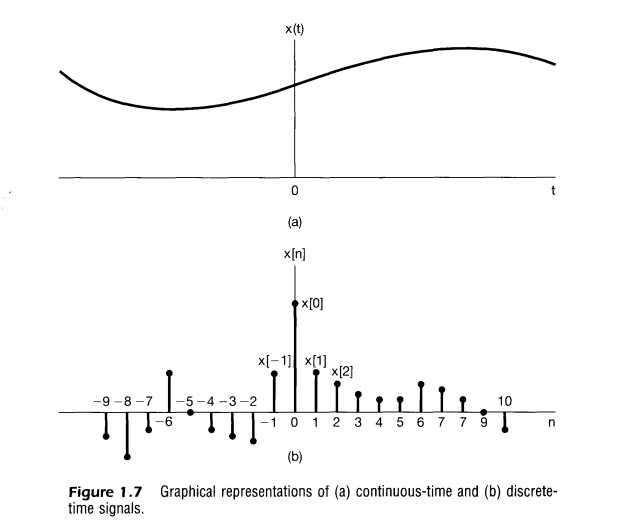
우함수 신호와 기함수 신호(even and odd signal)
우함수 신호 : $x(-t)=x(t), x[n]=x[-n]$를 만족하는 신호 ex) $\cos (t)$
기함수 신호 : $-x(t)=x(-t), -x[n]=x[-n]$를 만족하는 신호 ex) $\sin (t)$
임의의 신호는 기함수 신호와 우함수 신호 두개의 신호로 분리 될 수 있다.
즉, 임의의 신호는 반드시 어떤 우함수 신호와 기함수 신호의 합으로 표현 될 수 있다.
신호 $x(t)$를 짝수부분과 홀수부분으로 분리하면 아래와 같으며 유일하다.
짝수 부분 : $\displaystyle \mathscr E v\{x(t)\}=\frac{1}{2}[x(t)+x(-t)]$
$x(t)$와 $x(-t)$를 더하고 $2$로 나누어주면 기함수신호 성분은 모두 소거되고 우함수신호 만 남는다.
홀수 부분 : $\displaystyle \mathscr O d\{x(t)\}=\frac{1}{2}[x(t)-x(-t)]$
$x(t)$에 $x(-t)$를 빼고 $2$로 나누어주면 우함수신호 성분은 모두 소거되고 기함수신호 만 남는다.
$\blacksquare$
지수신호와 정현파신호(Exponential and Sinusoidal Signal)
연속시간 복소지수 신호와 정현파 신호(Continuous-Time Complex Exponential and Sinusoidal Signals)
복소지수 신호 : $x(t)=Ce^{at}(C,a \in \mathbb C)$
변수 $C$와 $a$의 값에 따라 복소지수는 몇 개의 다른 특성들을 나타낸다.
실지수신호(Real Exponential Signals)

위 그림처럼 $C$와 $a$가 실수라면 이경우에 $x(t)$는 실지수 라고 불린다. 그리고 실지수는 두가지 형태가 있다.
1. $a > 0$ 일 경우
$x(t)$는 시간이 증가할수록 증가하는 지수이다.
2. $a < 0$ 일 경우
$x(t)$는 시간이 증가할수록 감소하는 지수이다.
$\circ$ 주기적인 복소 지수 신호와 정현파 신호
$\displaystyle x(t)=e^{jw_0t}=\cos w_0t+j\sin w_0t$
이 신호는 주기적이다.
proof)
$\displaystyle e^{jw_0t}=e^{jw_0(t+T)}$
위 식을 정리하면
$\displaystyle e^{jw_0(t+T)}=e^{jw_0t}e^{jw_0T}=e^{jw_0t}$
등식이 성립하기 위해선
$\displaystyle e^{jw_0T}=1$ 이어야 한다.
$\displaystyle e^{jw_0T}=\cos w_0T + j \sin w_0T=1$
$\displaystyle w_0T=2\pi a (a\in \mathbb Z)$를 만족해야 한다.
$\displaystyle wT=2\pi f\frac{1}{f}=2 \pi$
$\therefore \cos w_0T=1, \sin w_0T=0$ 이므로 $\displaystyle x(t)=e^{jw_0t}=\cos w_0t+j\sin w_0t$ 는 주기신호이다


일반적인 정현파 신호
$\displaystyle x(t)=A\cos(w_0t+\phi)$
$e^{jw_0t}$는 아래와 같이 표현 가능함을 알고있다.
euler's formular : $e^{jw_0t}=\cos w_0t +j \sin w_0t$
그러므로
$\displaystyle \cos (w_0t+\phi )$와 $\displaystyle \sin (w_0t+\phi )$는 각각 $\displaystyle e^{j(w_0t+\phi )}$의 실수부와 허수부이다.
$$A\cos (w_0t+\phi)=A \mathfrak{Re} \left\{e^{j(w_0t+\phi)}\right\}\\
B\sin (w_0t+\phi)=B \mathfrak{Im} \left\{e^{j(w_0t+\phi)}\right\}$$
특히 $\cos(w_0t+\phi)$는 우함수이고, $\sin(w_0t+\phi)$는 기함수이기 때문에
$$A\cos (w_0t+\phi)=\mathscr E V\{Ae^{j\phi}e^{jw_0t}\}=\frac{A}{2} e^{j\phi} e^{jw_0t}+\frac{A}{2} e^{-j\phi} e^{-jw_0t}$$
$$B\sin (w_0t+\phi)=\mathscr O V\{Ae^{j\phi}e^{jw_0t}\}=\frac{A}{2} e^{j\phi} e^{jw_0t}-\frac{A}{2} e^{-j\phi} e^{-jw_0t}$$
$\displaystyle e^{jw_0t}$신호의 한 주기에 대한 총 에너지와 평균 파워를 계산하면
$$\begin{align*}
E_{period}&=\int_{0}^{T_0}\left|e^{jw_0t} \right|^2dt\\
&=\int_{0}^{T_0}1dt=T_0\\
P_{period}&= \frac{1}{T_0}E_{period}=1
\end{align*}$$
$\therefore$ 복소주기 지수신호는 아래처럼 유한한 평균파워를 지닌다.
$$P_{\infty}=\lim_{T \rightarrow \infty}\frac{1}{2T} \int_{-T}^{T} \left|e^{jw_0t} \right|^2 dt=1$$
고조파(Harmonic)
고조파란 원신호의 기본 주파수에 $k$를 곱하여 나오는 모든 신호들의 집합이다.
고조파와 관련된 복소지수집합은 하나의 양의 주파수 $w_0$의 모든 배수의 기본 주파수 들을 갖는 주기적인 지수집합이다.
$$\phi_k(t)=e^{jkw_0t},(k \in \mathbb Z)$$
고조파에 대한 실사용의 예는 악기에 들 수 있다.
음악에서 사용되는 기본 주파수의 정수배인 주파수들에서 음성 공기 압력의 변동으로 야기되는 톤을 나타내는것과 일치한다.
가령, 바이올린 같은 악기에서 한 줄의 떨림 패턴은 고조파와 관련된 주기적인 지수들의 중첩, 즉 가중된 합으로 나타낼수있다.

$\blacksquare$
$\circ$ 일반적인 복소 지수 신호
$Ce^{at}$의 경우 $C$는 극좌표형식, $a$는 직교좌표형식으로 표현된다.
$C=|C|e^{j\theta}. a=r+jw_0$
그러므로 $\displaystyle C=e^{at}=|C|e^{j\theta}e^{(r+jw_0)t}=|C|e^{rt}e^{(w_0t+\theta)}$
오일러 관계식에 의해
$displaystyle \begin{align*}
Ce^{at}&=|C|e^{rt} \cos (w_0t+\theta)+j|C|e^{rt}\sin(w_0t+\theta)\\
&=|C|e^{rt}\{\cos(w_0t+\theta)+j\sin(w_0t+\theta)\}\\
&=|C|e^{rt}A\cos(w_0t+\theta+\phi)
\end{align*}$
위는 지수적으로 크기가 변하는 정현파를 나타낸다.
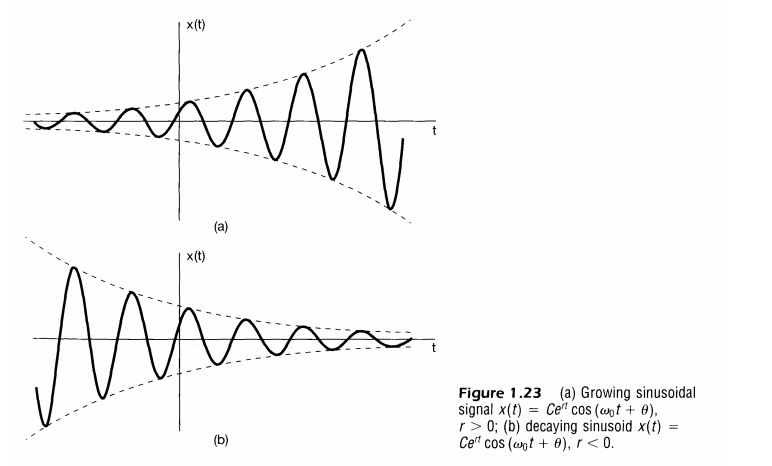
이산시간 복소지수 및 정현파 신호
복소 지수 신호는 아래와 같다
$\displaystyle \begin{align*}
x[n]&=C \alpha ^n &&(C,\alpha \in \mathbb C)&\\
&=Ce^{\beta n}&&(\alpha = e^\beta)&
\end{align*}$
$\alpha$와 $\beta$의 값에 따라 다양한 신호를 얻을 수 있다.
$\circ$ 실수 지수 신호
$C, \alpha \in \mathbb R$ 이면 아래의 형태중 하나를 취할 수 있다.
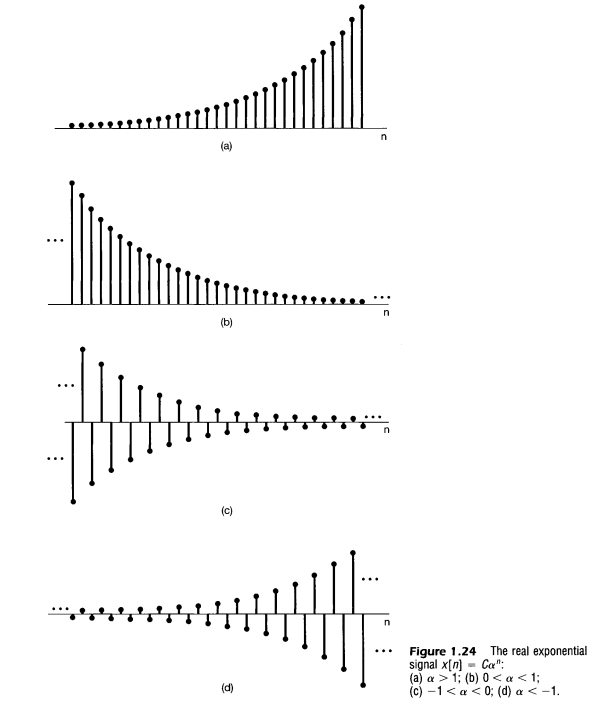
$\circ$ 정현파 신호
$\beta$가 무리수 일 경우 얻을 수 있는 신호이다.
$\displaystyle x[n]=Ae^{jw_0n}=A\cos w_0n + jA\sin w_0n=A \cos (w_0n+\phi)$
$A \cos (w_0n+\phi)$는 $Ae^{jw_0n}$의 실수부 이므로 아래처럼 표현 가능하다.
$\displaystyle A \cos (w_0n+\phi)=\frac{A}{2} e^{j\phi}e^{jw_0n}+\frac{A}{2}e^{-j\phi}e^{-jw_0n}$
정현파 신호는 무한한 총 에너지와 유한한 평균 파워를 지닌다.
$\circ$ 일반적인 복소지수신호
$C, \alpha \in \mathbb C$ 일 때 $C$와 $\alpha$를 극좌표형식으로 쓸 경우
$C=|C|e^{j\theta}$
$\alpha=|\alpha|e^{jw_0}$
$C\alpha^n=|C||\alpha|^n\cos(w_0n+\theta)+j|C||\alpha|^n\sin(w_0n + \theta)=|C||\alpha|^n e^{jw_0n}$
이다. $|\alpha|=1$일때, 복소 지수열의 실수부와 허수부는 정현파(sinusoidal)이다.
$|\alpha|<1$일때 정현파 신호가 지수적으로 감쇠하며 $|\alpha|>1$일때 신호는 지수적으로 증가함을 볼 수 있다.
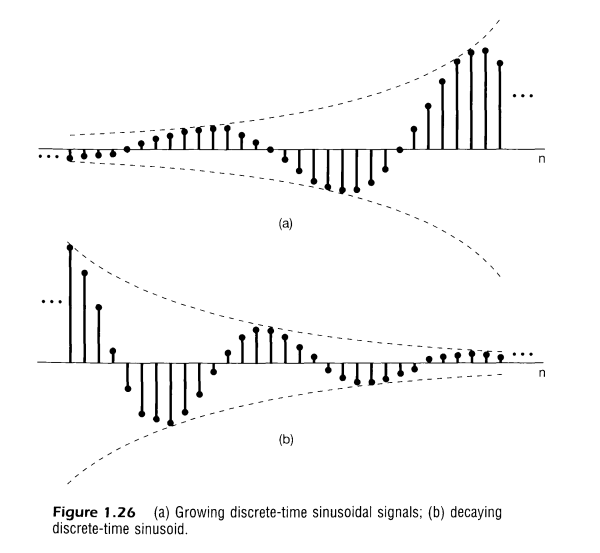
$n$에 단위가 없으면 $w_0$와 $\phi$는 모두 rad 단위를 갖는다.

이산시간 복소지수의 주기 특성(Periodicity Properties of Discrete-Time Complex Exponentials)
신호의 주기가 샘플링 주기의 배수와 일치한다면 모두 똑같은 파형을 가진다.
이는 이산시간 신호의 샘플링주기 때문이며 이때문에 이산시간 신호와 연속시간 신호의 가장큰 차이는 크게 2가지가 있으며
1) 주파수가 $w_0 \pm 2 \pi k$인 신호는 $w_0$인 신호와 같다.
가령 $w_0+2\pi$의 주파수를 가지는 아래의 신호를 확인하자
| $\circ$ 이산시간 | $\circ$ 연속시간 |
|
$e^{j(w_0+2\pi)n}=e^{jw_0n}e^{j2\pi n}, (n \in \mathbb Z)$ 즉, 주파수가 $w_0 \pm 2\pi k$인 신호와 $w_0$인 신호가 서로 같다. |
$e^{j(w_0+2\pi)t}=e^{jw_0t}e^{j2\pi t}, (t \in \mathbb R)$ t가 실수이므로 정현파 신호의 형태를 그대로 가져올 수 있음을 확인 할 수 있다. |
그러므로 이산시간 복소지수를 고려할때는
$2 \pi$길이의 주파수 구간만 고려하면 되고 이 안에서 $w_0$를 선택한다.
보통 $0 \leq w_0 < 2\pi$ 혹은 $-\pi < w_0 < \pi$를 이용한다.
그리고 $e^{j(w_0+2\pi)n}=e^{jw_0n}e^{j2\pi n}, (n \in \mathbb Z)$ 식에서 보이는것 처럼 신호 $e^{jw_0n}$의 $w_0$의 크기가 증가할수록 진동이 계속해서 증가하지는 않는다.

위 그림에서 보듯이 $w_0$을 0에서부터 증가시키면 신호는 $w_0=\pi$가 될때까지는 진동속도가 올라가지만 $w_0=2 \pi$에 이를때 까지는 진동률이 감소함을 볼 수 있다.
그리고 $k \pi$와 $(2-k)\pi$가 같은 파형을 가짐을 볼 수 있다.
2) 신호 $e^{jw_0n}$의 주파수 $w_0$가 $w_0N=2\pi m (m,N \in \mathbb Z)$를 만족한다면 이 신호는 주기적이며 그렇지 않다면 비주기적이다.
신호 $e^{jw_0n}$의 주기가 $N(>0)$이라면 아래 등식을 만족해야한다.
$e^{jw_0(n+N)}=e^{jw_0n}$
위 등식이 만족되기 위해선
$e^{jw_0N}=1$
이어야 한다. 그러기 위해선
$w_0N=2\pi m\;(m,N \in \mathbb Z), \frac{w_0}{2 \pi}=\frac{m}{N}$
위 조건을 만족해야한다.
즉, 신호 $e^{jw_0n}$의 주파수 $w_0$가 $w_0N=2\pi m (m,N \in \mathbb Z)$를 만족한다면 이 신호는 주기적이며 그렇지 않다면 비주기적이다.
| $e^{jw_0t}$ | $e^{jw_0n}$ |
| 서로 다른 $w_0$ 값에 따라 서로 다른 신호 | 2$\pi$ 배수만큼 떨어진 $w_0$에 대해서는 동일 신호 |
| 어던 $w_0$에 대해서도 주기적 | 어떤 $N>0$과 m 경우에 $w_0=2\pi m / N$이면 주기적 |
| 기본주파수 $w_0$ | 기본주파수 $w_0/m$ (m과 N의 공통인수가 없다고 가정) |
|
기본주기 $w_0=0$ : 정의 안됨 $w_0 \neq 0$ : $\frac{2 \pi}{w_0}$ |
기본주기 $w_0=0$ : 정의 안됨 $w_0 \neq 0$ : $m\frac{2 \pi}{w_0}$ |
'신호 및 시스템' 카테고리의 다른 글
| 2. 선형 시불변 시스템(LTI system) - 이산시간 LTI 시스템: 컨볼루션 합(Convolution Sum) (0) | 2020.04.18 |
|---|---|
| 2. 선형 시불변 시스템(LTI system) - 서론 (0) | 2020.04.18 |
| 1장. 연습문제 (0) | 2020.04.17 |
| 1. 연속시간 및 이산시간 시스템 (0) | 2020.03.28 |
| 1.단위 임펄스 및 단위 계단함수 (0) | 2020.03.26 |