| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 다익스트라
- Trie
- MYSQL
- Two Points
- 그래프
- Dijkstra
- Stored Procedure
- Brute Force
- SQL
- Hash
- String
- two pointer
- 스토어드 프로시저
- 이진탐색
- binary search
- DP
- union find
- Today
- Total
codingfarm
3. 변환-선형변환, 아핀변환, 함성, 좌표 변경 변환 본문
함수 $\tau$에 대하여 아래와 같은 성질이 성립하면, 그리고 오직 그럴때에만 $\tau$를 가리켜 선형변환(linear transformation)이라 부른다
$$\tau (u + v) = \tau (u) + \tau (v)$$
$$\tau(ku) = k \tau(u)$$
여기서 $u$와 $v$는 벡터이고, $k$는 스칼라이다.
비례(scaling)
물체의 크기를 바꾸는 효과를 내는 선형변환이다.
비례변환은 다음과 같이 정의된다.
$$S(x,y,z) = (s_xx, s_yy, s_zz)$$
이는 현재 좌표계를 기준으로, 벡터를 $x$축으로 $s_x$ 단위, $y$축으로 $s_y$단위, $z$축으로 $s_z$단위 만큼 비례한다.
선형 변환에 대한 표준행렬 S는 아래와 같다.
$$S = \begin{bmatrix} s_x & 0 & 0 \\ 0 & s_y & 0 \\ 0 & 0 & s_z \end{bmatrix}$$
이 행렬을 비례행렬(scaling matrix)라 한다.
비례행렬의 역은 아래와 같이 주어진다.
$$S^{-1} = \begin{bmatrix} 1/s_x & 0 & 0 \\ 0 & 1/s_y & 0 \\ 0 & 0 & 1/s_z \end{bmatrix}$$
회전
벡터 $\mathbb v$를 축 $\mathbb n$에 대해 회전하는 선형변환을 살펴본다.

축 $n = (x,y,z)$에 대해 $\theta$ 만큼 회전시키는 표준행렬은 아래와 같다.
$$R_n = \begin{bmatrix}
c+(1-c)x^2 & (1-c)xy +sz & (1-c)xz - sy \\
(1-c)xy - sz & c + (1 - c) y^2 & (1 - c)yz + sx \\
(1-c)xz + sy & (1-c)yz - sx & c + (1-c)z^2
\end{bmatrix}$$
$R_n$의 역은
$$R_n^{-1} = R_n^T = \begin{bmatrix}
c+(1-c)x^2 & (1-c)xy - sz & (1-c)xz + sy \\
(1-c)xy + sz & c + (1 - c) y^2 & (1 - c)yz - sx \\
(1-c)xz - sy & (1-c)yz + sx & c + (1-c)z^2
\end{bmatrix}$$
여기서 $c = cos \theta$이고 $s = sin \theta$ 이다.
$x$축이나 $y$축, $z$축에 대한 회전 행렬은 아래와 같다.
$$R_x = \begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & \cos \theta & \sin \theta & 0 \\
0 & - \sin \theta & \cos \theta & 0 \\
0 & 0 & 0 & 1
\end{bmatrix},
R_y = \begin{bmatrix}
\cos \theta & 0 & - \sin \theta & 0 \\
0 & 1 & 0 & 0 \\
\sin \theta & 0 & \cos \theta & 0 \\
0 & 0 & 0 & 1
\end{bmatrix},
R_z = \begin{bmatrix}
\cos \theta & \sin \theta & 0 & 0 \\
-\sin \theta & \cos \theta & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}$$
가령 $A = {A_x, A_y, A_z}$를 회전변환 하고 싶다면
$AR_n$ 곱을 통해 그 결과를 얻을 수 있다.
이동변환
우선 아핀변환부터 살펴보겠다.
아핀변환(affine transformation)
선형변환에 이동변환을 결합(합성)한 것이다.
벡터는 방향과 크기만 서술하는것이므로 위치와는 무관하다.
즉, 벡터는 이동에 대해 불변이어야하며, 이동은 오직 점에만 적용해야한다.
하지만 동차 좌표(homogeneous coordinate)라는 것을 이용하면 점과 벡터를 동일한 방식으로 다룰 수 있다.
동차 좌표는 3차원 벡터네 $w$성분을 추가한 네값쌍(4-tuple)의 형태인데, 주어진 동차좌표가 점을 나타내느냐 벡터를 나타내느냐는 이 $w$값이 결정한다.
구체적으로 말해서
1. 벡터를 나타내는 동차좌표는 $(x,y,z,0)$
2. 점을 나타내는 동차좌표는 $(x,y,z,1)$
로 표기한다.
점을 나타내는 동차좌표에서 $w = 1$로 설정해야 점의 이동 변환이 제대로 수행된다.
벡터를 나타내는 동차좌표에서 $w= 0$ 으로 해두어야 벡터에 대한 이동변환시 벡터의 성분들이 변하는 문제를 방지할 수 있다.
가령, 두 점 혹은 두 벡터의 차는 벡터가 된다
점 - 점 : $(q_x, q_y, q_z , 1) - (p_x, p_y, p_z, 1) = (q_x - p_x, q_y - p_y, q_z - p_z, 0)$
벡터 - 벡터$(v_x, v_y, v_z , 0) - (u_x, u_y, u_z, 0) = (v_x - u_x, v_y - u_y, v_z - u_z, 0)$
점에 벡터를 더하면 해당 점을 시작점으로 벡터만큼 이동한 새로운 점이 나온다.
$p + v = (p_x, p_y, p_z, 1) + (v_x, v_y, v_z , 0) = (p_x + v_x,p_y+v_y,p_z+v_z,1)$
그리고 벡터에 벡터를 더하면 새로운 벡터가 되지만, 점에 점을 더하는 연산은 불가능하다.
$\blacksquare$
아핀 변환의 정의와 행렬 표현
3차원 그래픽에 필요한 변환중에는 선형 변환으로는 서술 못하는 것들이 있다.
그래서 아핀변환이라는 좀 더 넓은 부류의 함수들을 도입해야 한다.
아핀변환은 선형변환에 이동벡터 $b$를 더한것이다. 이를 수식으로 표현하면 아래와 같다.
$$\alpha (u) = \tau (u) + b$$
이를 행렬로 표기하면
$$\alpha (u) = u A + b = [x,y,z]
\begin{bmatrix}
A_{11} & A_{12} & A_{13}\\
A_{21} & A_{22} & A_{23}\\
A_{31} & A_{32} & A_{33}
\end{bmatrix}
+ [b_x, b_y, b_z] = [x', y', z']$$
행렬 A는 선형변환의 표준행렬이다.
여기서 $w=1$인 동차좌표를 도입하면 아래처럼 좀더 간결하게 포현할 수 있다.
$$[x,y,z,1]
\begin{bmatrix}
A_{11} & A_{12} & A_{13} & 0\\
A_{21} & A_{22} & A_{23} & 0\\
A_{31} & A_{32} & A_{33} & 0\\
b_x & b_y & b_z & 1
\end{bmatrix}
= [x', y', z',1]$$
위 식에서 $4 \times 4$ 행렬을 아핀변환의 행렬표현이라 부른다.
벡터는 위치가 없으므로 벡터에 대해서는 $b$에 의한 이동은 적용받지 않게 된다.
$\blacksquare$
이동
주어진 인수를 그대로 돌려주는 변환을 항등변환(identity transformation)이라 한다.
즉, $I(u) = u$에서 변환$I$는 항등변환이다.
항등변환의 행렬표현은 단위행렬이다.
따라서 이동변환은 선형변환 부분이 하나의 단위행렬인 아핀변환이다.

가령 $u$를 $b$만큼 이동하고자 한다면
$$\tau(u) = uI + b = u + b$$
이경우 $\tau$를 아래와 같은 행렬료 표현할 수 있다.
$$T =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
b_x & b_y & b_z & 1
\end{bmatrix}$$
이러한 행렬 표현을 이동행렬(translation matrix)라 한다.
이동행렬의 역은 아래와 같다.
$$T =
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
-b_x & -b_y & -b_z & 1
\end{bmatrix}$$
$\blacksquare$
아핀변환의 기하학적 해석
강체(rigid body) 변환을 생각해보자.
강체변환이란 변환시 물체의 형태가 유지되는 변환이다.
$\tau$가 회전변환, $b$가 변위벡터라면
강체변환을 아래와같은 아핀변환으로 서술 가능하다.
$$\alpha(x,y,z) = \tau(x,y,z) + b = x\tau(i) + y\tau(j) + z\tau(k) + b$$
$i = (1,0,0), \; j = (0,1,0), \; k (0,0,1)$ 인 단위벡터이다.
이를 동차 좌표와 행렬로 표기하면 아래와 같다.
$$[x,y,z,w]
\begin{bmatrix}
\leftarrow & \tau (i) & \rightarrow \\
\leftarrow & \tau (j) & \rightarrow \\
\leftarrow & \tau (k) & \rightarrow \\
\leftarrow & b & \rightarrow
\end{bmatrix}
= [x', y', z', w]$$
아래 그림을 보면 위 등식의 기하학적 의미를 쉽게 알 수 있다.
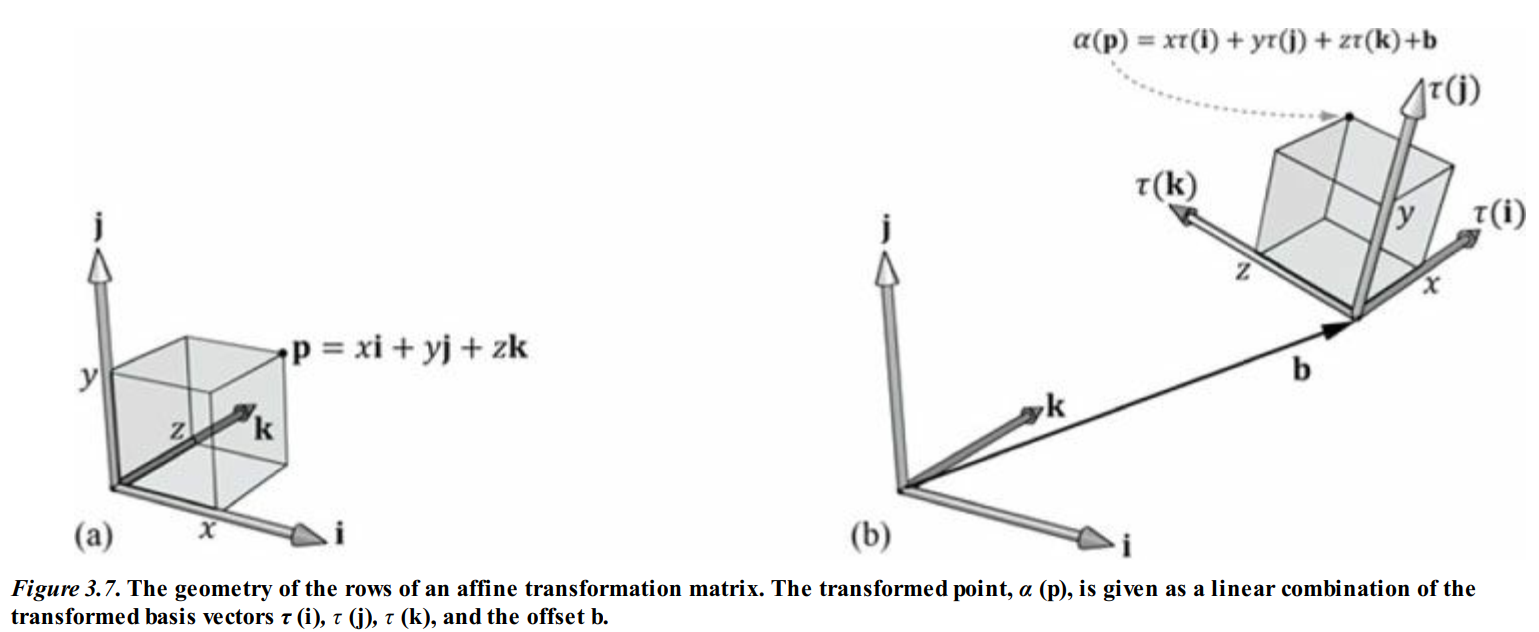
$\tau$는 회전변환이므로 $i,j,k$사이의 각도가 $\tau(i),\tau(j),\tau(k)$에서도 유지된다.
이는 비례나 기울기 변환에도 적용된다.
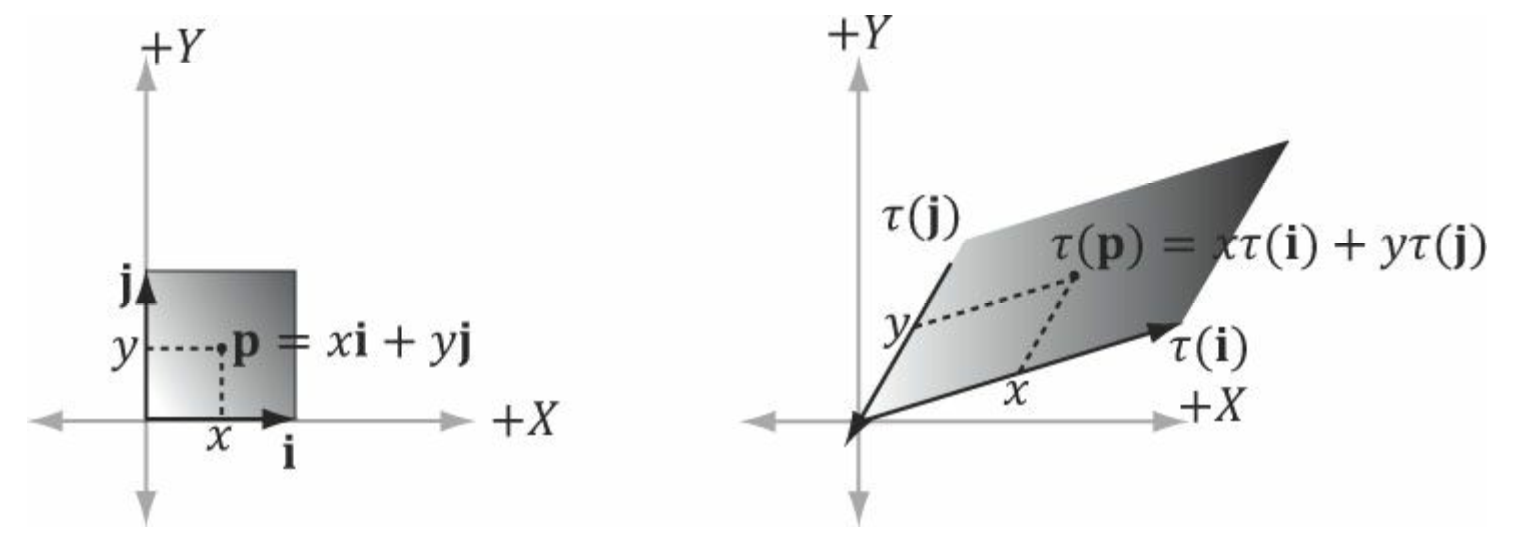
위에서 변환된 점 $\tau (p) = (x,y)$는 변환된 기저벡터 $\tau (i)$와 $\tau (j)$의 선형 결합으로 간주된다.
선형변환 : $p = xi+yj+zk \rightarrow \alpha(p) = x \tau(i) + y \tau(j) + z\tau(k) + b$
$\blacksquare$
변환들의 합성
$S$가 비례행렬이고 $R$이 회전행렬, $T$가 이동행렬이라고 하자,
$i = 0,1, \cdots, 7$인 여덟 정점 $V_i$ 들로 이루어진 입방체의 각 정점에 이 세변환을 연달아 적용하려 한다.
이를 수행하는 자명한 방법은 다음처럼 각 행렬들을 하나씩 차례대로 적용하는 것이다.
$i=0,1,\cdots,7$에 대해 $((v_iS)R)T = (v_i'R)T = v_i''T = v_i'''$
하지만 행렬 곱셈은 결합법칙을 만족하므로, 아래처럼 표기해도 된다.
$i=0,1,\cdots,7$에 대해 $v_i(SRT) = v_i'''$
행렬 $C=SRT$를, 세가지 변환을 하나의 전체적인 변환으로 감싼 행렬로 간주할 수 있다.
여러 행렬을 곱함으로써 전체적인 변환을 하나로 합치는 효과를 낼 수 있다.
이러한 합성을 통해 성능 개선에 큰 영향을 줄 수 있다.
'computer graphics > DX12 book' 카테고리의 다른 글
| 4. COM(Component Object Model) (0) | 2021.01.11 |
|---|---|
| 4. Direct3D 초기화 - 개요 (0) | 2021.01.11 |
| 3. 변환 - DirectXMath 라이브러리의 변환 함수들 (0) | 2020.11.22 |
| 3. 변환 - 좌표 변경 변환(change of coordinate transformation) (0) | 2020.11.22 |
| 2. 행렬 대수 (0) | 2020.11.21 |


