| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 다익스트라
- Two Points
- Hash
- SQL
- Brute Force
- 이진탐색
- 스토어드 프로시저
- DP
- Stored Procedure
- binary search
- MYSQL
- Trie
- union find
- Dijkstra
- two pointer
- 그래프
- String
- Today
- Total
codingfarm
3. 변환 - 좌표 변경 변환(change of coordinate transformation) 본문
3. 변환 - 좌표 변경 변환(change of coordinate transformation)
scarecrow1992 2020. 11. 22. 00:41한 기준계의 점 또는 벡터의 상대적인 좌표를 다른 기준계에 상대적인 좌표로 변환하는 것을 좌표 변경 변환이라 한다.
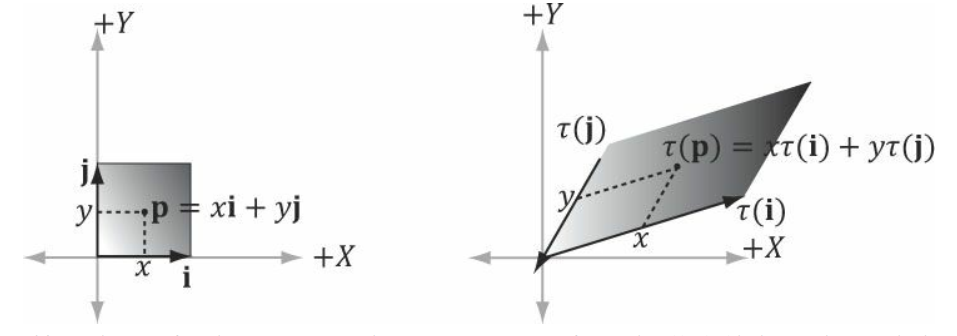
위그림에서 $i$축과 $j$축에 대해 존재하던 상대 좌표 $p$가 있다.
축 $i$와 $j$가 변형될경우, $\tau(i)$와 $\tau(j)$에 대해 점 $p$도 변형되어 $\tau(p)$에 위치하게 된다.
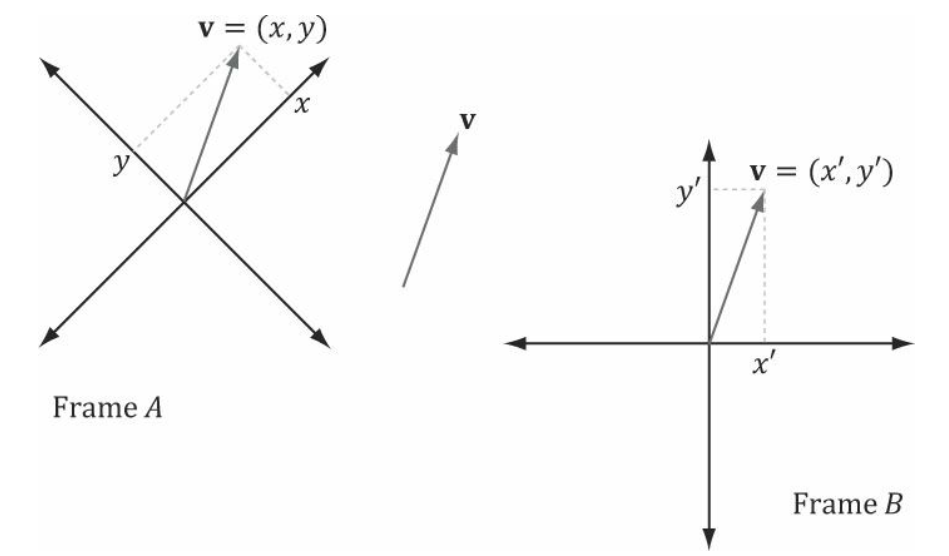
3차원 컴퓨터 그래픽에서는 여러개의 좌표계를 사용하는 경우가 많으므로, 한 좌표계에서 다른 좌표계로의 변환 방법에 익숙할 필요가 있다.
위치는 벡터가 아니라 점의 속성이며, 점에 대한 좌표계변환과 벡터에 대한 좌표계 변환은 서로 다르다.
$\blacksquare$
벡터

두 좌표계 $A$와 $B$, 그리고 벡터 $p$가 있다.
좌표계 $A$에 상대적인 $p$의 좌표가 $p_A=(x,y)$라고 할 때, 좌표계 $B$에 상대적인 $p$의 좌표 $p_B = (x',y')$를 구하고자 한다.
즉, 문제는 아래와 같다.
어떤 기준계에서 상대적인 벡터를 나타내는 좌표가 주어젔을때, 그것을 다른 어떤 기준계에 상대적인 좌표로 변환하려면 어떻게 해야 할까?
$$p = xu + yv$$
여기서 $u$와 $v$는 각각 좌표계 $A$의 $x$축과 $y$축 방향의 단위벡터이다.
이를 좌표계 $B$에 대해 나타내면
$$p_B = xu_B + yv_B$$
따라서, $p_A(x,y)$가 주어졌을 때, 만일 좌표계 $B$에 상대적인 $u$와 $v$의 좌표들을 안다면,
다시말해 $u_B = (u_x, u_y)$와 $v_B=(v_x, v_y)$를 알면, 항상 p_B=(x',y')을 구할 수 있다.
이를 3차원으로 일반화하면, $p_A = (x,y,z)$라고 할 때
$$p_B = xu_B + yv_B + zw_B$$
이다. 여기서 $u_B, v_B, w_B$는 좌표계 $B$의 방향 벡터들을 좌표계 $A$의 방향 벡터들로 표현한 벡터들이다.
$\blacksquare$
점
점에 대한 좌표 변경 변환은 벡터에 대한것과 약간 다르다.

점 $\mathbb p$를 다음과 같은 공식으로 표현 할 수 있다.
$$\mathbb p = x\mathbb u + y\mathbb v + \mathbb Q$$
여기서 $u$와 $v$는 각각 좌표계 $A$의 $x$축과 $y$축 방향의 단위벡터이고, $\mathbb Q$는 좌표계 $A$의 원점이다. 이 수식의 점과 벡터들을 좌표계 $B$에서 표현하면 아래와 같다.
$$\mathbb p_B = x\mathbb u_B + y\mathbb v_B + \mathbb Q_B$$
따라서, $\mathbb p_A = (x,y)$가 주어졌을 때 만일 좌표계 $B$에 상대적인 벡터 $u$와 $v$, 원점 $Q$의 좌표들을 안다면, 다시말해 $\mathbb u_B = (u_x, u_y), \mathbb v_B = (v_x, v_y), \mathbb Q_b(Q_x, Q_y)$를 알면, 항상 $\mathbb p_B = (x', y')$을 구할 수 있다.
이를 3원으로 일반화하면, $\mathbb p_A = (x,y,z)$라 할때
$$p_B = x u_B + y v_B + Q_B$$
이다. 여기서 $u_B, v_B, w_B$는 각각 좌표계 $A$의 $x,y,z$ 축 방향 단위벡터들을 좌표계 $B$에 상대적으로 표현한 벡터들이고 $Q_B$는 좌표계 $A$의 원점을 좌표계 $B$에 상대적으로 표현한것이다.
$\blacksquare$
행렬 표현
벡터와 점에대한 좌표변경변환공식을 정리하면 아래와 같다.
$\bullet$ 벡터 : $(x',y',z') = x \mathbb u_B + y \mathbb v_B + z \mathbb w_B$
$\bullet$ 점 : $(x',y',z') = x \mathbb u_B + y \mathbb v_B + z \mathbb w_B+ \mathbb Q_B$
동차좌표를 통해 벡터와 점을 하나의 공식으로 처리할 수 있다.
$$(x', y', z', w) = x \mathbb u_B + y \mathbb v_B + z \mathbb w_B + w \mathbb Q_B$$
어떤 $1 \times n$ 행벡터 $\mathbb u$와 어떤 $n \times m$ 행렬 $\mathbb A$에 대해 곱 $\mathbb{uA}$는 $\mathbb A$의 행벡터들과 $\mathbb u$의 스칼라 계수들의 선형결합이다.
$$[u_1, \cdots, u_n]
\begin{bmatrix}
A_{11} & \cdots & A_{1m} \\
\vdots & \ddots & \vdots \\
A_{n1} & \cdots & A_{nm}
\end{bmatrix}
=
[u_1, \cdots, u_n]
\begin{bmatrix}
\uparrow & & \uparrow \\
A_{1,*} & \cdots & A_{n,*} \\\
\downarrow & & \downarrow
\end{bmatrix}
=
u_1A_{1,*} + \cdots + u_nA_{n,*}$$
그러므로 $[x',y',z',w]$는 아래처럼 나타낼 수 있다.
$$\begin{align*}
[x',y',z',w] &= [x,y,z,w]
\begin{bmatrix}
\leftarrow & \mathbb u_B & \rightarrow \\
\leftarrow & \mathbb v_B & \rightarrow \\
\leftarrow & \mathbb w_B & \rightarrow \\
\leftarrow & \mathbb Q_B & \rightarrow
\end{bmatrix}\\ \\
&=[x,y,z,w]
\begin{bmatrix}
\mathbb u_x &\mathbb u_y & \mathbb u_z & 0 \\
\mathbb v_x & \mathbb v_y &\mathbb v_z & 0 \\
\mathbb w_x &\mathbb w_y &\mathbb w_z & 0 \\
Q_x & Q_y & Q_z & 1
\end{bmatrix}\\ \\
&= x \mathbb u_B + y \mathbb v_B + z \mathbb w_B + wQ_b
\end{align*}$$
여기서 $Q_B$와 $u_B, v_B, w_B$은 좌표계 $A$의 원점과 축들을 좌표계 $B$에 상대적인 동차 좌표로 표현한 것이다.
위 식의 $4 \times 4$ 행렬을 좌표 변경 행렬(change of coordinate matrix)라 부른다.
그리고 이 행렬이 수행하는 변환을 가리켜서 좌표계 $A$의 좌표를 좌표계 $B$의 좌표로 변환한다(convert) 또는 사상한다(map)라고 말한다
$\blacksquare$
결합법칙과 좌표 변경 행렬
세 좌표계 $F,G,H$가 있다고 하자.
$A$가 $F$에서 $G$로의 좌표계 변경 행렬이고 $B$가 $G$에서 $H$로의 좌표계 변경행렬 이라고 하자.
한 벡터의 좌표계 $F$에 상대적인 좌표 $p_F$를 좌표계 $H$에 상대적인 좌표 $p_H$로 변환하는 방법은 아래와 같다.
$$(p_FA)B = p_H$$
$$(p_G)B = p_H$$
그런데 행렬의 곱셈은 결합법칙을 만족하므로 $(p_FA)B=p_H$를 다음과 같이 표기해도 된다.
$$p_F(AB)=p_H$$
여기서 행렬 곱 $C=AB$를 $F$에서 직접 $H$로 가는 좌표계 변경 행렬이라고 볼 수 있다.
이러한 합성(compositon)은 성능에 영향을 미친다.
하지만 행렬의 곱은 교환법칙이 성립하지 않으므로 좌표계의 변경 순서 즉, 행렬의 곱셈 순서는 꼭 유지 해야한다.
$\blacksquare$
역행렬과 좌표 변경 행렬
$p_B$를 벡터 $p$의 좌표계 $B$ 기준 좌표($B$를 기준으로 한 $p$의 좌표)라 하자. 그리고 $M$이 좌표계 $A$에서 $B$로의 좌표 변경 행렬이라 하자. 이럴경우 $p_B = p_A M$을 만족하는 좌표 $p_A$를 구하고자 한다.
다른말로하면, 이번에는 좌표계 $A$에서 좌표계 $B$로의 사상이 아니라 좌표계 $B$에서 $A$로의 사상을 나타내는 좌표변경 행렬이 필요하다. $M$이 가역행렬이라 할 때 (즉 $M^{-1}$이 존재 할 때), $p_A$를 아래처럼 구할 수 있다.
$$\begin{align*}
p_B &= p_AM \\
p_B M^{-1} &= p_AMM^{-1} \\
p_B M^{-1} &= p_AI \\
p_B M^{-1} &= p_A
\end{align*}$$
따라서 행렬 $M^{-1}$은 좌표계 $B$에서 $A$로의 좌표 변경 행렬이다.


'computer graphics > DX12 book' 카테고리의 다른 글
| 4. COM(Component Object Model) (0) | 2021.01.11 |
|---|---|
| 4. Direct3D 초기화 - 개요 (0) | 2021.01.11 |
| 3. 변환 - DirectXMath 라이브러리의 변환 함수들 (0) | 2020.11.22 |
| 3. 변환-선형변환, 아핀변환, 함성, 좌표 변경 변환 (0) | 2020.11.21 |
| 2. 행렬 대수 (0) | 2020.11.21 |


