| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- 이진탐색
- String
- SQL
- two pointer
- Stored Procedure
- Two Points
- 다익스트라
- Brute Force
- DP
- Trie
- MYSQL
- 그래프
- Dijkstra
- binary search
- Hash
- union find
- 스토어드 프로시저
- Today
- Total
codingfarm
연속형 확률분포 - 연속형 확률변수(Continuous Random Variables of The Continuous Type ) 본문
연속형 확률분포 - 연속형 확률변수(Continuous Random Variables of The Continuous Type )
scarecrow1992 2020. 4. 21. 16:32연속형 확률분포(Continuous Distribution)-연속형 확률변수(Continuous Random Variables of The Continuous Type )
구간 혹은 구간들의 합인 공간 $S$를 가지는 연속형 확률변수 $X$의 $pdf$는 다음의 조건을 만족하는 적분 가능한함수 $f(x)$이다.
(a) $f(x)>0,\;\;\;\;x \in S$
(b) $\int_S f(x) dx=1$
(c) $(a,b) \subseteq S$ 이라면 사상$\{a<x<b\}$의 확률은 아래와 같다.
$$P(a<X<b)=\int_{a}^{b}f(x)dx$$
연속형 확률변수 $X$가 구간 $[a,b]$,$-\infty < a< b< \infty$,로부터 임의로 선택되는 하나의 점의 위치를 나타낸다고 한다. 이 실험이 공정하게 진행된다면, 하나의 점이 구간 $[a,x]$, $a \leq x<b$, 로부터 선택될 확률은 $\dfrac{x-a}{b-a}$이다.
확률은 구간의 길이에 비례하므로 $X$의 $cdf$는
$$F(x)=p(X \leq x)=\begin{cases}0,&x<a\\\dfrac{x-a}{b-a},&a\leq x < b\\1,&b \leq x\end{cases}$$
그리고
$$F(x)=\int_{-\infty}^{x}f(y)dy$$
여기서
$$f(x)=\dfrac{1}{b-a},\;\;\;\;\;\;\; a\leq x\leq b$$
즉, $F'(x)=f(x)$ 이고 $f(x)$를 $X$의 확률 밀도 함수(Probability Density Function; pdf) 라고 한다.
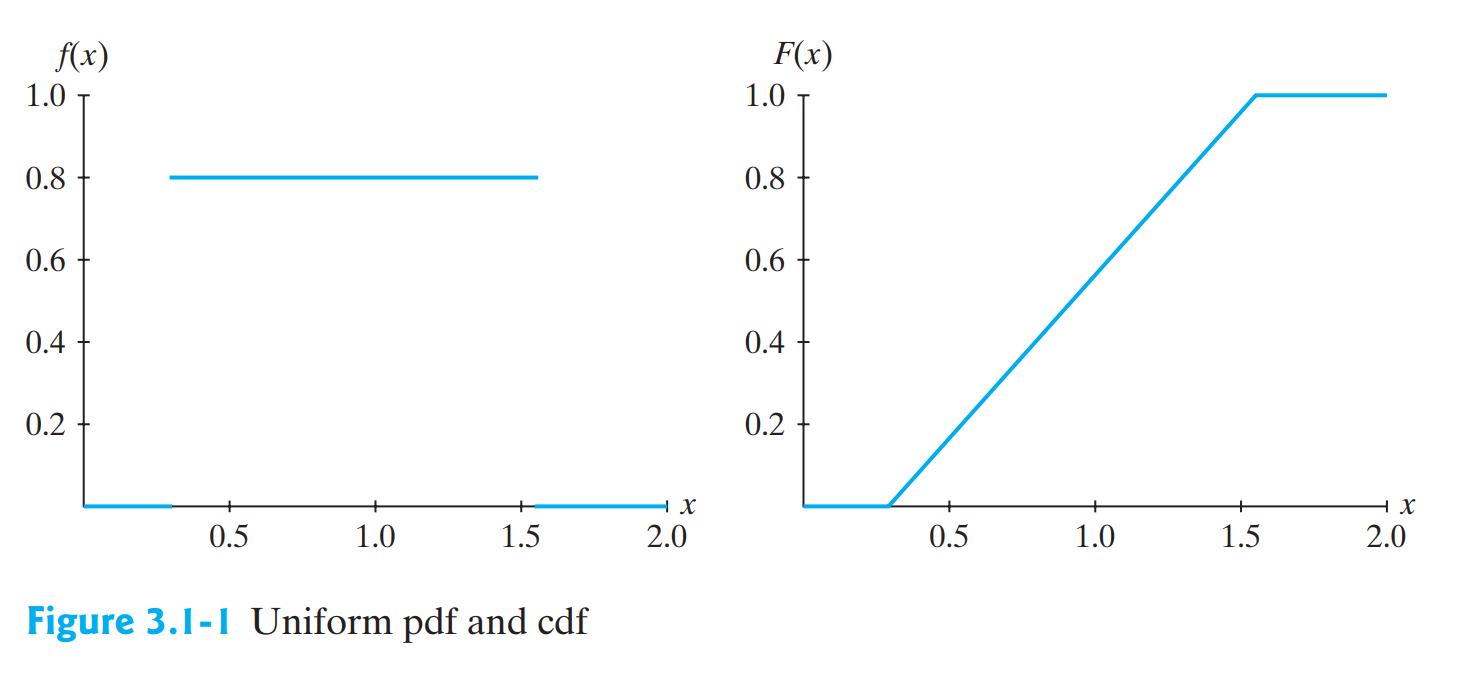
확률변수 $X$의 $pdf$가 공간위에서 상수와 같다면 확률변수 $X$는 균일분포(uniform distribution)/직사각형분포(rectangular distribution)을 가지며 특히 구간 $[a,b]$의 공간위에서
$$f(x)=\frac{1}{b-a}\;\;\;\;\;\;,a<x<b\;\;\;\;\;,-\infty<a<b<\infty$$
와 같은 균일분포를 $X \sim U(a,b)$로 표기한다.
연속형 확률변수 $X$의 $cdf$를 $X$의 $pmf$로 나타내면
$$F(X)=p(X \leq x)=\int_{-\infty}^{x}f(t)dt,\;\;\;\;-\infty<x<\infty$$
$F'(x)$가 존재하는 모든 $x$에 대하여 $F'(x)=f(x)$가 성립한다.
$\blacksquare$
연속형 확률변수의 $pmf$
이산형 확률변수의 $pmf$ $f(x)$는 $f(x)=P(X=x)$이므로 최대 1의 한계를 가지나, 연속형 확률변수의 $pdf$는 한계를 가질 필요가 없다.
그러나 $pdf$와 $x$축 사이의 면적은 반드시 1이어야 한다.
$$\int_{-\infty}^\infty f(x)dx=1,\;\;\;\;\;\;a<x<b$$
연속형 확률변수의 $pdf$는 무조건 연속일 필요가 없다. 하지만 연속형 확률변수의 $cdf$는 항상 연속함수이다.
연속형 확률변수 $pmf$의 평균과 분산
$$\begin{align*}
\mu&=E(X)=\int_{-\infty}^{\infty}xf(x)dx\\
\sigma^2&=Var(X)=E[(X-\mu)^2]=\int_{-\infty}^{\infty}(x-\mu)^2f(x)dx
\end{align*}$$
연속형 확률변수 X의 적률생성함수(moment generating function; mgf)
$$M(t)=\int_{-\infty}^{\infty}e^{tx}f(x)dx,\;\;\;\;\;-h<t<h$$
$$\begin{align*}
\mu&=M'(0)\\
\sigma^2&=M''(0)-[M'(0)]^2
\end{align*}$$
$h>0$인 $-h<t<h$에서 적률생성함수가 유한이면 적률생성함수는 분포에 대해 유일하다.
참고
이산형과 연속형의 경우에 $r$차 적률 $E(X^r)$이 존재하고 유한이라면 보다 낮은 모든 차수의 적률, $E(X^k),\;\;\;k=1,2,\cdots,r-1$이 존재하고 유한이다. 그러나 그 역은 성립하지 않는다.
$\blacksquare$
$U(a,b)$ 분포의 평균, 분산
$$\mu=\frac{a+b}{2},\;\;\;\;\;\sigma^2=\frac{(b-a)^2}{12}$$
$$M(t)=\begin{cases} \dfrac{e^{tb}-e^{ta}}{t(b-a)},&t \neq 0\\ 1&t=0 \end{cases}$$
$\blacksquare$
제100$p$백분위수(percentile)
$X$가 $pdf$ $f(x)$와 $cdf$ $F(x)$를 갖는 연속형 확률 변수라 한다.
제100$p$백분위수는 아래식
$$\color{blue}p=\int_{-\infty}^{\displaystyle\pi_{\color{blue}p}}f(x)dx=F(\pi_{\color{blue}p})$$
를 만족시키는수 $\pi_p$이다.
$$\begin{align*}
제1사분위수(the\;first\;quartile) &:q_1=\pi_{0.25}\\
중위수(median),제2사분위수(the\;second\;quartile) &:m=\pi_{0.5}=q_2\\
제3사분위수(the\;third\;quartile)&:q_3=\pi_{0.75}
\end{align*}$$
'통계학 > 수리통계학' 카테고리의 다른 글
| 연속형 확률분포 - 감마분포(The Gamma Distributions) (0) | 2020.04.23 |
|---|---|
| 연속형 확률분포 - 지수분포(The Exponential Distributions) (0) | 2020.04.21 |
| 포아송분포표(Poisson Distribution Table) (0) | 2020.04.14 |
| 이산형 확률분포(Discrete Distribution) - 포아송분포(Poisson Distribution) (0) | 2020.04.14 |
| 이산형 확률분포(Discrete Distribution) - 음이항분포(negative binomial distribution) (0) | 2020.04.12 |











