| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- DP
- Hash
- SQL
- two pointer
- 스토어드 프로시저
- Dijkstra
- 그래프
- Trie
- binary search
- Brute Force
- String
- Two Points
- 다익스트라
- MYSQL
- Stored Procedure
- union find
- 이진탐색
- Today
- Total
codingfarm
26. 좌표 변환 본문
0. 소개
world 좌표계를 기준으로 주어지는 오브젝트들을 화면에 수월하게 그리기 위해선 카메라의 좌표를 기준으로 표현한 후, 화면에 출력하기 위해 view port 좌표계로 다시한번 변환할 수 있어야 한다.
이를 위해 좌표변환에 대해 알아야 한다.
1. 선형 변환
정의 : $\mathbb R^n$에 속하는 임의의 벡터$u$, $v$와 스칼라 $c$에 대하여
1) $T(u+v) = T(u) + T(v)$
2) $T(cu) = cT(u)$
위 2개 조건을 만족하는 변환$T: \mathbb R^n \rightarrow \mathbb R^m$ 을 선형변환 이라 한다.
즉, 선형변환 $T$는
$$T(c_1v_1+c_2v_2) = c_1T(v_1) +c_2T(v_2)$$
위 등식을 만족한다.
1-1. 행렬 표현(표준 행렬)
$A$가 $m \times n$ 행렬 일때
$$T_A(x) = Ax, \;\; x \in \mathbb R^n$$
로 정의되는 행렬변환 $T_A: \mathbb R^n \rightarrow \mathbb R^m$은 선형변환이다.
$$e_1=(1,\; 0,\; 0,\; \cdots 0)\\
e_2=(0,\; 1,\; 0,\; \cdots 0)\\
e_3=(0,\; 0,\; 1,\; \cdots 0)\\
\vdots \\
e_n= (0,\; 0,\; 0,\; \cdots 1)$$
일 때
$$A=\begin{bmatrix}\; T(e_1) \; | \; T(e_2) \; | \cdots |\; T(e_n) \end{bmatrix}$$
위와 같은 행렬 $A$를 선형변환 $T$의 표준행렬이라 한다.
선형변환 $T:\mathbb R^n \rightarrow \mathbb R^m$이 주어질 때
$T(p) = pA, \; p \in \mathbb R^n$
를 만족하면 $A$를 선형변환 $T$의 표준행렬 또는 행렬표현이라 한다.
컴퓨터 그래픽스에서 쓰이는 기초적인 선형 변환은 아래와 같다.
1-2. 비례
비례변환 $S$는 아래처럼 정의된다
$S(x,y,z) = (S_x x, S_y y, S_z z)$
위 선형변환을 바탕으로 표준행렬을 구하면
$S(\hat i) = (S_x, 0,\; 0)\\
S(\hat j) = (0,\; S_y, 0)\\
S(\hat k) = (0,\; 0,\; S_z)$
$s =
\begin{bmatrix}
\leftarrow & s(\hat i) & \rightarrow \\
\leftarrow & s(\hat j) & \rightarrow \\
\leftarrow & s(\hat k) & \rightarrow \\
\end{bmatrix}
=
\begin{bmatrix}
S_x & 0 & 0 \\
0 & S_y & 0 \\
0 & 0 & S_z \\
\end{bmatrix}
$
그러므로
$ S(x,y,z) =
\begin{bmatrix}
x & y & z
\end{bmatrix}
\begin{bmatrix}
S_x & 0 & 0 \\
0 & S_y & 0 \\
0 & 0 & S_z \\
\end{bmatrix}$
2. 아핀변환
3. 좌표변환
용어
${}^BP$ : $B$ 좌표계 기준 점 $P$의 좌표
${}^BP$의 성분 : $({}^BP_X , \; {}^BP_Y,\;{}^BP_Z)$
$\hat X_B,\; \hat Y_B,\; \hat Z_B$ : $B$ 좌표계의 각 주축들
${}^A\hat X_B,\; {}^A\hat Y_B,\; {}^A\hat Z_B$ : $B$ 좌표계의 각 주축들 ($A$ 좌표계 기준)
점 ${}^BP$의 좌표를 좌표계 $A$를 기준으로 변환하기
1. 임의의 좌표계
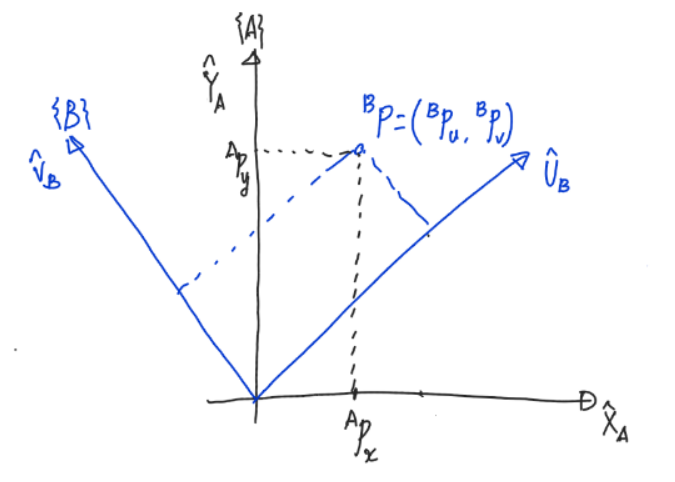
${}^B \hat U$와 ${}^B \hat V$는 ${}^A \hat X$와 ${}^A \hat Y$에 대응된다.
${}^BP$ 를 ${}^AP$ 로 변환하는 방법에 대해 알아본다.
우선 ${}^BP$를 $A$의 $\hat X_A$ 기준으로 바꾸어 본다. (${}^A P_x$를 구한다.)
${}^B P_u \cdot {}^AU_B$와 ${}^B P_v \cdot {}^AV_B$ 를 $\hat X_A$에 투영한 길이의 합과 같다.
즉, 각 벡터간의 내적의 합이라 볼 수 있다.
$${}^A P_x = ({}^B P_u \cdot {}^A \hat U_B)\cdot \hat X_A + ({}^B P_v \cdot {}^A \hat V_B)\cdot \hat X_A = \hat X_A({}^B P_u \cdot {}^A \hat U_B + {}^B P_V \cdot {}^A \hat V_B)$$
이때 $\hat X_A$는 $Y$ 성분의 값이 0이므로 ${}^A \hat U_B$와 ${}^A \hat V_B$의 $\hat X_A$성분만 곱해지게 되어 사실상 스칼라 끼리의 곱이라 볼 수 있다.
즉,
$${}^A \hat U_B = ({}^A U_{B.x} \; , \; {}^A U_{B.y} \; , \; {}^A U_{B.z})$$
$${}^A \hat V_B = ({}^A V_{B.x} \; , \; {}^A V_{B.y} \; , \; {}^A V_{B.z})$$
라 할때
$$\begin{align*}
{}^AP_x &= {}^BP_u \cdot {}^AU_{B.x} + {}^BP_v \cdot {}^AV_{B.x}\\
&= [{}^BP_u , \; {}^BP_v]
\begin{bmatrix} {}^AU_{b.x} \\ {}^AV_{b.x} \end{bmatrix}
\end{align*}$$
이런식으로 ${}^AP_y$ 도 구하면
$$\begin{align*}
{}^AP_y &= {}^BP_u \cdot {}^AU_{B.x} + {}^BP_v \cdot {}^AV_{B.x}\\
&= [{}^BP_u , \; {}^BP_v]
\begin{bmatrix} {}^AU_{b.y} \\ {}^AV_{b.y} \end{bmatrix}
\end{align*}$$
그러므로 ${}^AP$는
$${}^AP = [{}^AP_x,\; {}^AP_y] =
[{}^BP_u, \; {}^BP_v]
\begin{bmatrix}
{}^AU_{B.u} & {}^AU_{B.v}\\
{}^AV_{B.u} & {}^AV_{B.v}
\end{bmatrix}$$
편의상 $B$ 좌표계의 주축을 $\hat U_B, \; \hat V_B$로 표현했찌만 $\hat X_B, \hat Y_B$로 표현하면
$${}^AP = [{}^AP_x,\; {}^AP_y] =
[{}^BP_x, \; {}^BP_y]
\begin{bmatrix}
{}^AU_{B.x} & {}^AU_{B.y}\\
{}^AV_{B.x} & {}^AV_{B.y}
\end{bmatrix}$$
이를 3차원으로 확장하면
$$\begin{align*}
{}^AP &= [{}^AP_x,\; {}^AP_y, \; {}^AP_z] =
[{}^BP_x, \; {}^BP_y, \; {}^BP_z]
\begin{bmatrix}
\leftarrow & {}^A\hat X_B & \rightarrow \\
\leftarrow & {}^A\hat Y_B & \rightarrow \\
\leftarrow & {}^A\hat Z_B & \rightarrow
\end{bmatrix}
\\
&= {}^BP \cdot {}^A R_B
\end{align*}$$
2. 좌표계 이동
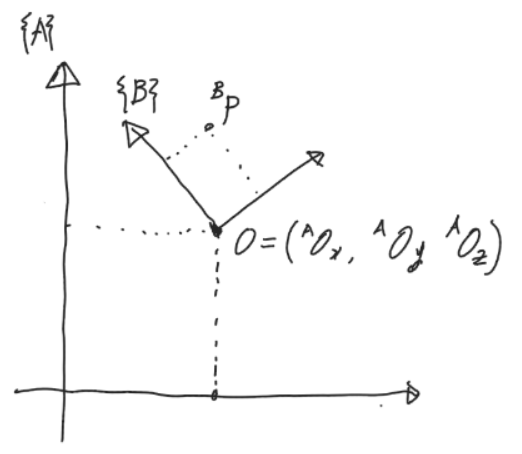
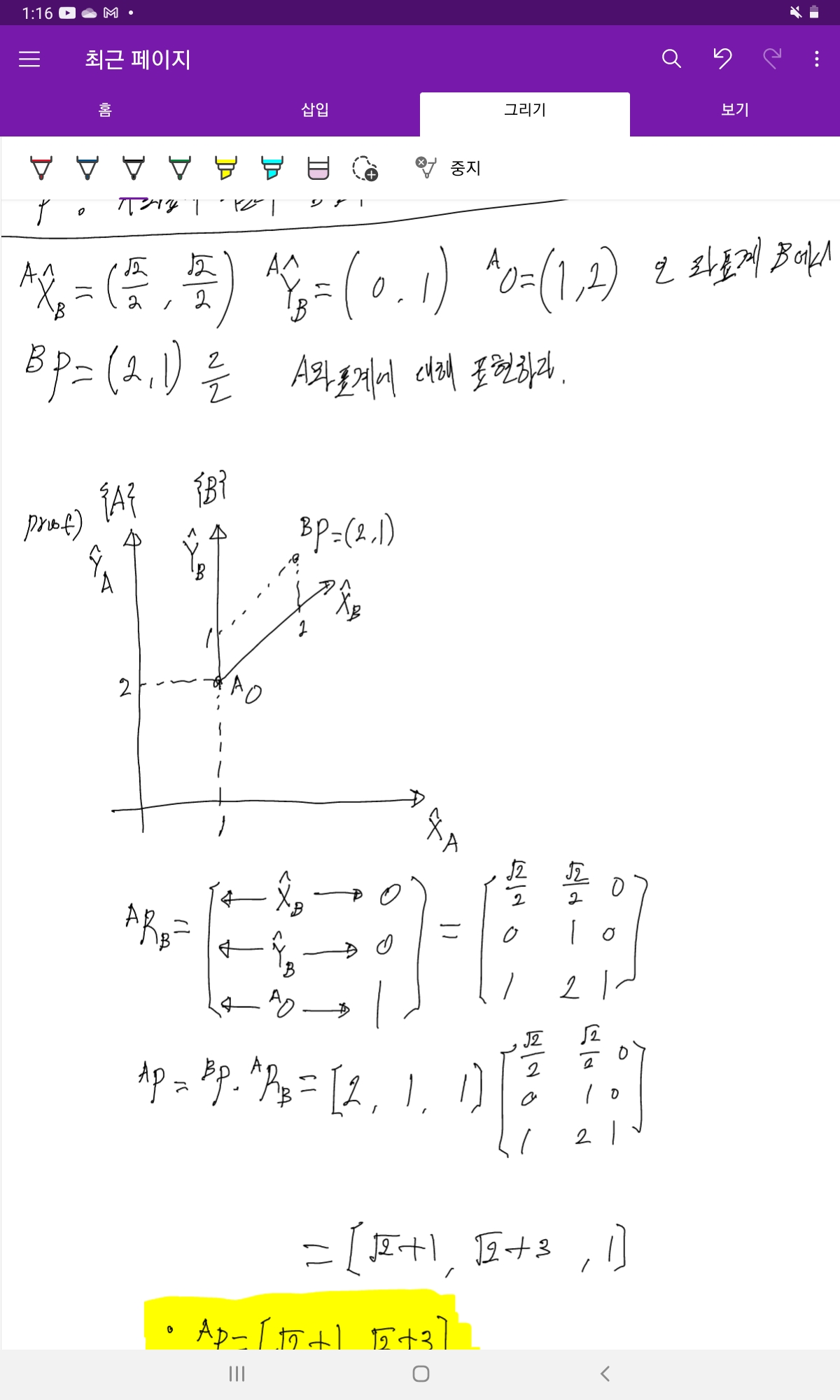
$B$좌표계의 원점이 $A$좌표계 기준 ${}^AO$위치에 있을경우 ${}^BP$를 $A$좌표계에 대해 표현하면 아래와 같다.
$${}^AP={}^BP \cdot {}^AR_B + {}^AO$$
2. 카메라
'computer graphics > DirectX12' 카테고리의 다른 글
| 27-1. 텍스처적용 예제 코드 (0) | 2021.09.22 |
|---|---|
| 27. 텍스처 적용(Texturing) (0) | 2021.09.19 |
| 24. 색이 변하는 구 (0) | 2021.08.19 |
| 23. Cube 그리기 (0) | 2021.08.10 |
| 22. 삼각형 그리기 2 (0) | 2021.08.05 |