| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
Tags
- MYSQL
- Two Points
- 다익스트라
- two pointer
- Hash
- SQL
- DP
- String
- Dijkstra
- binary search
- Stored Procedure
- 그래프
- Brute Force
- 스토어드 프로시저
- union find
- Trie
- 이진탐색
Archives
- Today
- Total
codingfarm
충돌 여부 검사 본문
어휘력이 모자라서 충돌 이외의 적절한 말을 모르겠다.
임의의 범위를 가진 데이터들이 주어질때, 특정 데이터의 범위와 겹치치는 것들을 필터링 하는 방법에 대해서 정리해보았다.
1 : 1
1:1 대응을 검사하는 방법은 간단하다.
가령 [al, ar], [bl, br] 과 같은 범위를 가지는 데이터가 주어젔을 때, 해당 데이터가 서로 겹처지는지 확인하는 방법은 아래와 같다.
$$al \leq br \; \& \& \; bl \leq ar $$
위 조건이 만족된다면 해당 데이터는 겹처지는 것이다.
참고로 겹처지지 않을 조건은 아래와 같다
$$al > br \; || \; bl > ar $$
1 : N
그렇다면, 하나의 데이터가 주어질때 여러 데이터들과의 충돌 여부를 판정하는 방법은 무엇일까?
하나하나 대응하면서 비교하는 방법으로 $O(N)$의 효율로 해결하는 방법도 있지만 이진탐색을 쓰면 $O(\log_2 N)$ 의 효율로 해결 된다.
특정 데이터가 다른 데이터와 겹치는 경우는 총 4가지이며, 안겹치는 경우는 2가지이다.
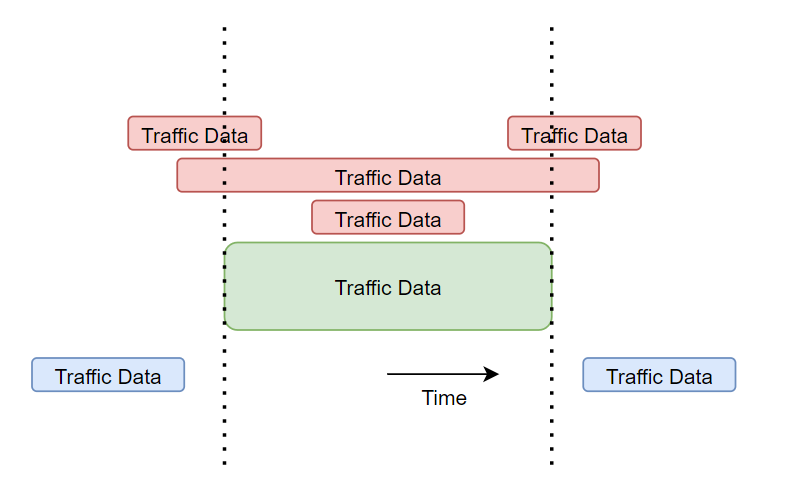
이진탐색을 기반으로 겹치는 데이터들만을 선별하는 작업은 상당히 까다롭다.
그러므로 우리는 겹치지 않는 데이터들만을 선별할것이다.
알고리즘은 아래와 같다.
- 트래픽 데이터들을 시작점과 끝점을 key로써 정렬한 벡터 별개의 벡터들을 각각 만든다(nodes_from, nodes_to)
- nodes_from에서 기준 트래픽의 끝점을 기준으로 오른쪽으로 분류된 데이터들을 구한다.
- 기준 트래픽의 끝점을 기준으로 nodes_from에 upper_bound를 적용하여 나온 지점에서 end 까지의 길이를 구한다.
- nodes_to 에서 기준 트래픽의 시작점을 기준으로 왼쪽으로 분류된 데이터들을 구한다.
- 기준 트래픽의 시작점을 기준으로 nodes_to에 lower_bound를 적용하여 나온 지점에서 begin 까지의 길이를 구한다.
정렬된 데이터의 슬라이싱은 아래 정보를 참고하면 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
|
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
class Node {
public:
int from, to;
Node(int from, int to) : from(from), to(to) {}
Node() : Node(-1, -1) {}
friend ostream& operator<<(ostream& os, const Node& rhs) {
os << "from : " << rhs.from << " , to : " << rhs.to;
return os;
}
};
bool CompFrom(const Node& lhs, const Node& rhs) {
return lhs.from < rhs.from;
}
bool CompTo(const Node& lhs, const Node& rhs) {
return lhs.to < rhs.to;
}
int main(void) {
vector<Node> nodes_from, nodes_to;
for (int i = 0; i < 30; i++) {
int from = rand() % 50;
int to = from + (rand() % 10);
nodes_from.push_back(Node(from, to));
nodes_to.push_back(Node(from, to));
}
sort(nodes_from.begin(), nodes_from.end(), CompFrom);
sort(nodes_to.begin(), nodes_to.end(), CompTo);
cout << "<< nodes_from>> " << endl;
for (int i = 0; i < nodes_from.size(); i++)
cout << i << " >> " <<nodes_from[i] << endl;
cout << "\n\n";
cout << "<< nodes_to >>" << endl;
for (int i = 0; i < nodes_to.size(); i++)
cout << i << " >> " << nodes_to[i] << endl;
Node pivot(30, 35);
vector<Node>::iterator it;
cout << "\n\n\n";
it = lower_bound(nodes_to.begin(), nodes_to.end(), Node(30, 30), CompTo);
cout << it - nodes_to.begin() << endl;
it = upper_bound(nodes_from.begin(), nodes_from.end(), Node(35,35), CompFrom);
cout << nodes_from.end() - it << endl;
return 0;
}
|
cs |
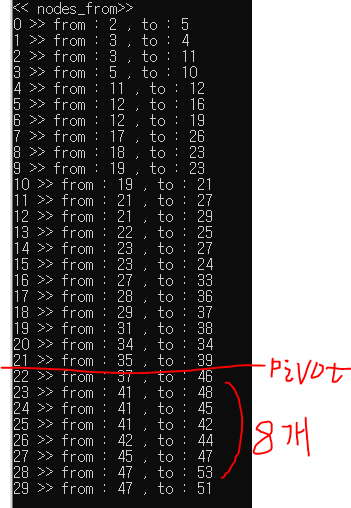
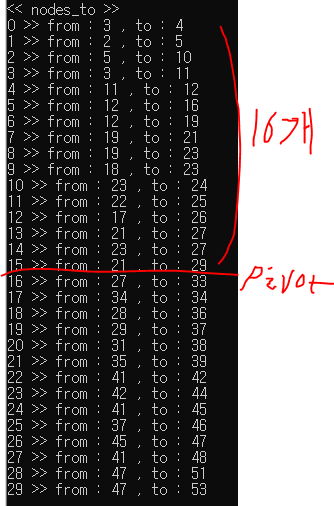

$30 - (16 + 8) = 6$개가 안겹치는것을 알 수 있다.
'Algorithm & Data structure > 이론' 카테고리의 다른 글
| 그래프 문제 모음 (0) | 2021.04.23 |
|---|---|
| StrTok (0) | 2021.04.22 |
| 정렬된 데이터를 이진탐색으로 슬라이싱 하기(lower_bound, upper_bound) (0) | 2021.04.21 |
| Dijkstra, Bellman-Ford, Floyd-Warshall (0) | 2021.04.20 |
| 비트연산 (0) | 2021.04.19 |
Comments


